¿En qué consiste la inferencia estadística? Protocolo de inferencia estadística - parte 1

La primera parcial de la asignatura de Estadística Aplicada (746) contempla los primeros cuatro objetivos, todos relacionados con el tema de inferencia estadística. Bien sea si realizamos inferencia por medio de intervalos de confianza (objetivo 1), contraste de hipótesis de una población (objetivo 2), contraste de hipótesis de dos poblaciones (objetivo 3) o tests de bondad de ajuste o con tablas de contingencia utilizando estadísticos chi-cuadrado (objetivo 4), hay un procedimiento (protocolo) que debemos seguir para resolver los problemas de inferencia estadística que se presentan en la evaluación de estos objetivos. Continuen leyendo más abajo para ver de que se trata.

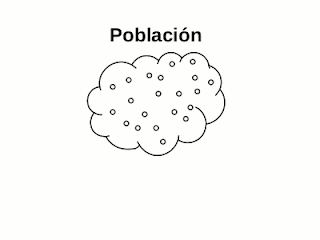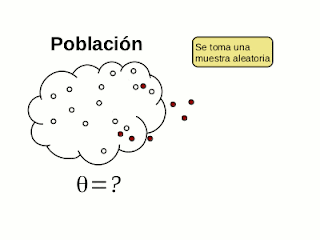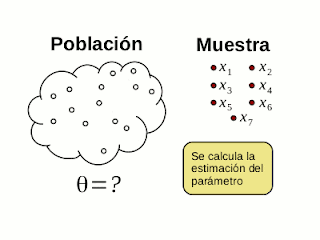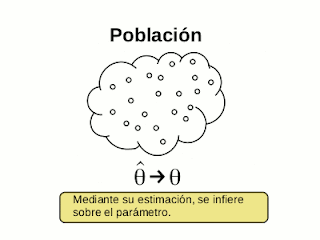
Antes de continuar con el protocolo para resolver los problemas de inferencia estadística tipo preguntas de examen, es preciso antes darles un paneo sobre la inferencia estadística - un poquito de teoría y conceptos. La inferencia estadística se crea para estudiar un conjunto de objetos (llamado población) que no podemos abarcar en su totalidad y en consecuencia, nos vemos obligados a tomar una muestra de ese conjunto para inferir sobre sus características. Para hablar en términos más operacionales, del conjunto de elementos o individuos que conforman la población extraemos un atributo o característica numérica que estudiaremos bajo la óptica de una variable aleatoria. Es decir, explicamos matemáticamente toda la variabilidad y complejidad de esa característica observada estudiándola como una variable aleatoria que tiene una distribución de probabilidad (generalmente desconocida) con unos parámetros también desconocidos. Así por ejemplo, las variables aleatorias exponenciales (con una distribución exponencial) generalmente explican más o menos adecuadamente los tiempos de espera entre eventos, las normalmente distribuidas explican fenómenos naturales como talla o peso, las de bernoulli explican fenómenos con características binarias (si/no, macho/hembra, etc.) y así con muchas otras distribuciones de probabilidad.

Aún si sabemos o tenemos una idea razonable de cual es la familia de distribuciones de probabilidad que mejor se caracteriza a la variable bajo estudio, tendríamos otro problema: ¿cuál es el valor de los parámetros poblacionales de esa distribución de probabilidad? Es decir, si sabemos que los tiempos de espera entre votantes sucesivos en una cola de votación es exponencialmente distribuidos, no conoceríamos la tasa lambda de esa distribución. Otro ejemplo: si sabemos que en un proceso de laminados se producen laminas cuyo espesor es normalmente distribuido, necesitaríamos conocer el valor de la media y de la desviación estándar (los dos parámetros poblacionales de la distribución normal). En los ejercicios que aparecen en los libros de texto de un curso de probabilidad, los parámetros poblacionales nos eran dados y nos pedían calcular probabilidades, lo cual era relativamente fácil porque conocíamos todas las características de la distribución de probabilidad en cuestión.

Pero la vida real no es como la pinta un libro de texto y entonces nosotros mismos tendríamos que estimar los valores de los parámetros poblacionales. Para eso es la inferencia estadística. Dicho sea de paso, la inferencia estadística sirve hasta para verificar si una variable observada se ajusta a una determinada familia de distribuciones de probabilidad o inclusive, para verificar si dos variables categóricas asociadas a un mismo individuo de la población son independientes entre sí (esto se hace en el objetivo 4 con los contrastes de hipótesis chi-cuadrados).

Si se trata de estimar el valor de un parámetro poblacional, existen tres formas de hacerlo: 1) estimación puntual, 2) estimación por intervalos de confianza o 3) estimación por contraste de hipótesis (o tests de hipótesis). Como ya dijimos al principio, los intervalos de confianza se evalúan en el objetivo 1 y los objetivos 2 al 4 evalúan contrastes de hipótesis. Permítanme hablarles entonces de la estimación puntual.

De acuerdo al parámetro que deseamos estimar, debemos de escoger el estimador apropiado. Un estimador es un estadístico, que a su vez es simplemente una función de la muestra. Los estimadores se utilizan para estimar o aproximarnos al verdadero valor de un parámetro porque son insesgados (su valor esperado es el valor del parámetro que pretenden estimar) y porque tienen poca varianza. Con esto quiero decir que los estimadores son variables aleatorias, que tienen a su vez una distribución de probabilidades, un valor esperado, una varianza, etc. Los estimadores son variables aleatorias porque cuando obtenemos distintas muestras, el valor del estimador varia de acuerdo a la muestra y como las muestras son aleatorias, el estimador varia aleatoriamente - de ahí que es una variable aleatoria. Es preciso fijar bien esta idea: Según la inferencia estadística clásica, los estimadores son variables aleatorias pero los parámetros, aunque sean desconocidos, son cantidades constantes y por lo tanto no son variables aleatorias.

En el curso de estadística aplicada estudiamos las formas de estimar la media poblacional (\(\mu\)), la varianza (\(\sigma^2\)), el parámetro de proporción (\(p\)) y la diferencia de las medias o de proporciones (\(\mu_1-\mu_2\) o \(p_1-p_2\) respectivamente). El tipo de parámetro que estamos estimando dicta nuestra escogencia del estimador que usaremos. Así, para estimar la media poblacional \(\mu\) utilizamos la media muestral \(\overline{X}=\frac{1}{n} \sum_{i=1}^n X_i\). Para la proporción utilizamos \(\hat{p}=\frac{1}{n} \sum X_i\) (\(\hat{p}\) se llama "p-techo" y los \(X_i\)'s en este caso son variables binarias tipo 0/1 para denotar la presencia o ausencia de un atributo en un individuo de la muestra). Para la varianza utilizamos como estimador \(S^2=\frac{\sum{(X_i-\overline{X})^2}}{n-1}\) y para la diferencia de las medias utilizamos, naturalmente, \(\overline{X_1}-\overline{X_2}\). Pueden constatar que en todo caso, los estimadores se calculan exclusivamente en función de la muestra (los \(X_i\)'s) y no se necesita ninguna otra información adicional.

Para obtener una estimación puntual de un parámetro sólo debemos calcular el valor correspondiente del estimador enchufando los valores de nuestra muestra (los \(X_i\)'s) en la fórmula del estimador y calcular su valor numérico. Pero recordemos que como la muestra es aleatoria, podemos obtener distintas estimaciones según distintas muestras. Es decir, en la estimación puntual hay un error inherente de aproximación al verdadero valor del parámetro, si bien todos estos estimadores "tienden en promedio" al verdadero valor del parámetro. El problema con la estimación puntual es que no nos ofrece ninguna cota o cuantificación de ese error. Por eso utilizamos otros métodos de estimación como lo son la estimación por intervalos o los tests de hipótesis.

En la estimación por intervalos de confianza, utilizamos la estimación del parámetro calculada según una muestra como centro de un intervalo cuya amplitud depende del nivel de confianza y de la variabilidad del estimador (recuerde que el estimador, siendo una variable aleatoria, tiene una varianza). En la medida en que el nivel de confianza, que generalmente es un porcentaje alto como 90%, 95% o 99%, sea mayor, el intervalo de confianza será mas amplio. En contraposición, mientras menor variabilidad tenga el estimador, el intervalo de confianza será mas estrecho.

Como investigadores nosotros quisiéramos tener intervalos muy estrechos porque estos nos permiten precisar más el valor de un parámetro. Esto podría lograr disminuyendo el nivel de confianza, pero de esta forma no estaríamos tan seguros que el intervalo en cuestión contenga el verdadero valor del parámetro. Por otro lado, si queremos aumentar la precisión de nuestra estimación, lo más conducente es tomar muestras de mayor tamaño (si esto es posible), porque mientras mayor sea el tamaño de la muestra, menor será la variabilidad del estimador.

Los intervalos de confianza de nivel de confianza \(1-\alpha\) no se interpretan afirmando que "este intervalo contiene al verdadero valor del parámetro con una probabilidad \(1-\alpha\)". Recuerden que los parámetros no son variables aleatorias y no podemos hacer afirmaciones probabilísticas respecto a ellos- un intervalo de confianza específico determinado a partir de una muestra específica contendrá o no al verdadero valor del parámetro poblacional y nunca sabremos cuál es el caso. Más bien, deberíamos de interpretar un intervalo de confianza del siguiente modo: si tomásemos muchísimas muestras aleatorias independientes y del mismo tamaño, la proporción \(1-\alpha\) de los intervalos de confianza construidos de la misma manera contendrían al verdadero valor del parámetro. El valor de \(\alpha\) vendría siendo entonces una medida del error en nuestra estimación.

Otra forma de hacer inferencia estadística con alguna medida de error es mediante el contraste de hipótesis. Para realizar un contraste de hipótesis, debemos indicar una hipótesis nula y una hipótesis alternativa. La hipótesis nula, denotada por \(H_o\) es una afirmación respecto parámetro desconocido sobre el cual hacemos inferencia y siempre toma la forma de una ecuación:

\[H_0: \theta=\theta_0\]

En algunos textos se indican las hipótesis nulas como desigualdades no estrictas (\(\leq\) o \(\geq\)), pero para poder llevar a cabo el contraste de hipótesis siempre debemos asumir que, bajo la hipótesis nula, el valor del parámetro desconocido \(\theta\) es exactamente igual a \(\theta_0\). Las hipótesis nulas se indican a veces como desigualdades no estrictas para señalar que el verdadero valor de \(\theta\) puede ser mayor/menor o igual que \(\theta_0\) sin que ello constituya un motivo para rechazar \(H_0\)- en la práctica nunca podríamos saber si \(\theta\) es exactamente igual a \(\theta_0\) en base a una muestra limitada de la población. Y ya que mencioné la palabra rechazar, debo decirles que sólo hay dos cosas que podemos hacer con una hipótesis nula: rechazarla o no rechazarla.

Cuando rechazamos una hipótesis nula, lo hacemos a favor de la hipótesis alternativa. La hipótesis alternativa, denotada por \(H_a\), es aquella afirmación que el investigador supone como cierta cuando ha rechazado la hipótesis nula y siempre se específica como una desigualdad estricta: bien sea \(H_a: \theta>\theta_0\), \(H_a: la \theta<\theta_o\) o \(H_a: \theta\neq\theta_0\). La hipótesis alternativa generalmente es lo que el investigador desea afirmar ulteriormente: siempre nos interesará saber si un parámetro es significativamente mayor, significativamente menor o significativamente distinto de un valor dado.

Más arriba les indiqué que sólo podemos rechazar o no rechazar una hipótesis nula. ¿Porqué en vez de "no rechazar", no decimos "aceptar" la hipótesis nula? La razón es que \(\theta\) podría no ser exactamente igual a \(\theta_0\), pero tampoco encontramos evidencia empírica (ie. evidencia muestral), según la cuál \(\theta\) sería significativamente menor, mayor o distinta de \(theta_0\). "Aceptar" la hipótesis nula equivaldría a afirmar que el valor de \(theta\) es exactamente igual a \(\theta_0\) cuando la evidencia muestral sólo nos indica que no hay diferencia significativa.

El trasfondo filosófico de la inferencia estadística mediante contraste de hipótesis se inspira mucho en la filosofía de Karl Popper, quien afirmaba que la construcción del conocimiento científico avanza refutando teorías o modelos de fenómenos reales. Cuando un modelo científico se "desvía" o no "predice" adecuadamente la evidencia empírica que hemos recabado, debemos decir que ese modelo no sirve o ha sido falseado (se ha comprobado su falsedad). Mientras no consigamos evidencia empírica contraria, no podemos afirmar que la realidad fenomenológica ulterior es exactamente como nuestro modelo la describe. Todo lo contrario: los modelos o las teorías científicas simplemente son descripciones más o menos adecuadas a la realidad observada mientras no se produzca evidencia de lo contrario.

Si la hipótesis nula es \(H_0: \theta=\theta_0\) y la hipótesis alternativa es \(H_a: \theta\gt\theta_0\), ¿significa esto que debemos rechazar \(H_0\) para cualquier valor del estimador \(\hat{\theta}\) mayor que \(\theta_0\)? No necesariamente. Según se dice en el argot estadístico, solo rechazaríamos \(H_0\) para valores de \(\hat{\theta}\) significativamente mayores que \(\theta_0\). La significatividad o el valor crítico para \(\hat{\theta}\) más allá del cual rechazamos la hipótesis nula depende de la medida del error, o nivel de significancia;, denotado por \(\alpha\) que el investigador estará dispuesto a tolerar. Recuerden que después de todo, \(\hat{\theta}\) es una variable aleatoria y si para una muestra dada, el valor de la estimación dista mucho de su media teórica según \(H_0: \theta=\theta_o\), entonces pueden ocurrir dos cosas: 1) \(H_0\) no es falsa pero acabamos de observar algo que tiene muy poca probabilidad \(\alpha\) de ocurrir o 2) \(H_0\) es falsa. Naturalmente, nos decantamos por la segunda opción, pero al hacerlo así, sabemos que podríamos estar cometiendo un error (el de rechazar una hipótesis nula verdadera) y hemos asumido una cota de tolerancia para ese error, que es el nivel de significáncia \(\alpha\).

Suficiente teoría por hoy. En otra entrada, les indicaré cómo ponemos todo esto en práctica para resolver problemas de inferencia estadística como los que se presentan en los exámenes.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.