Universidad Nacional Abierta Matemáticas El Tigre

Como seguramente ustedes saben, los trabajos prácticos de estadística pasaron a ser evaluaciones formativas desde hace algunos semestres. A partir de entonces, el objetivo 1 de Estadística General (745) se evalúa en la primera parcial y en la integral. Aunque ya no es necesario entregar un trabajo práctico cómo tal ni recibirá una calificación departe mía, yo les recomendaría realizar las actividades contempladas en el enunciado del trabajo, que fueron publicadas aqui. La razón de mi recomendación es porque en este semestre, las actividades del trabajo práctico contemplan la elaboración de diagramas de caja y de torta. Mi olfato docente me obliga a avisarles sobre esto e invitarlos a que continúen leyendo esta entrada, donde realizaremos juntos las actividades propuestas, no vaya a ser que las gráficas de tortas y de caja los agarren desprevenidos este semestre...

Continuamos con la serie de entradas sobre la visualización de datos, esta vez complementando un poco lo dicho sobre las gráficas de torta en la entrada pasada. ¿Cuándo deben o no usarse? ¿Cómo se deben usar?

En el semestre pasado 2012-1, la data del trabajo práctico versaba sobre un estudio de nutrición infantil donde se estudiaban varios factores conjuntamente como el Índice de Masa corporal, el peso, la estatura y la actividad física, entre otros. Para la asignatura de Estadística General (745), se requería, entre otras cosas, elaborar una gráfica de torta para la variable X7 - el índice de actividad física. A continuación muestro una típica gráfica de estas. Nótese que en el ejemplo de abajo, la gráfica de tortas es tridimensional, por lo cuál le hice observaciones al estudiante según las explicaciones en la entrada anterior. Para el trabajo final, los estudiantes re-elaboraron estas gráficas de torta en dos dimensiones, con lo cual dieron cumplimiento a la actividad correspondiente requerida en el enunciado del trabajo. Sin embargo - y con la presión del semestre ya dejada atrás, le invito a echar un segundo vistazo a esta gráfica. Aparte de la tridimensionalidad, ¿nota algún otro problema con esta gráfica?

Es necesario considerar el tipo de variable o la escala de X7. Si observa la leyenda a la derecha, verá que los niveles o valores del índice de actividad física son: sedentario, ligera, moderada, alta y muy alta. En efecto, la variable X7 se refiere a la intensidad o la frecuencia de actividad física de los individuos de la muestra. Podemos establecer comparaciones de orden entre estos niveles de actividad física. Por ejemplo, una persona con actividad moderada tiene menos actividad física que otra persona cuyo nivel de actividad es "alta". En resumen, X7 es una variable de escala ordinal. ¿Qué tiene esto que ver con las gráficas de torta?

En teoría, las gráficas de torta permiten visualizar el valor modal de una muestra. El valor modal es aquel con mayor frecuencia y por lo tanto el sector correspondiente en la gráfica de torta se verá más grande. Sin embargo, la variable X7 es una variable ordinal. Sus niveles tienen una jerarquía, un orden de menor a mayor. Gracias a ese orden jerárquico de sus niveles, la variable X7 tiene mediana, aparte de tener moda. Por cierto, la moda de esta variable es "actividad física alta" y su mediana es "actividad física moderada".

La gráfica de torta de arriba es deficiente. No logra comunicar toda la estructura jerárquica de orden que la variable X7 posee por ser una variable ordinal. En efecto, en una circunferencia no hay ningún punto privilegiado, no hay un cero natural, pues dejaría de serlo al rotar la circunferencia. Si uno recorre la circunferencia en cualquier dirección, regresa al punto de partida y por lo tanto en una circunferencia tampoco hay una dirección que esté asociada con "más de algo" o "menos de algo". Es decir, en una circunferencia no podemos reflejar ninguna jerarquía de orden. Si la gráfica de torta no es el tipo de gráfica más adecuada para resumir visualmente esta variable, ¿cuáles otros tipos de gráfica deberíamos de considerar?

La gráfica de barras es una alternativa natural para visualizar variables de escala ordinal cómo la variable X7. Si en el eje de las abscisas disponemos los niveles de X7 de menor a mayor (en la gráfica de arriba los niveles de actividad tienen una codificación numérica de 1.0 a 1.8) y hacemos corresponder los valores de las frecuencias en el eje de las ordenadas, las alturas de las barras encima de cada nivel de las abscisas nos permite visualizar la forma de la distribución de la variable X7. Aparte de poder visualizar la moda tal como en la gráfica de tortas, una gráfica de barras permite visualizar la asimetría, la dispersión y la forma general de la distribución de frecuencias, lo cual no podíamos hacer con una gráfica de tortas. Ampliando un poco más esta gráfica, podríamos por ejemplo señalar la clase mediana.

Sin embargo, sobre este último punto surge una inquietud respecto a si no existirá otro tipo de gráfica más "informativa" para variables de escala ordinal. Un tipo de gráfica que permita señalar la diferencia entre la moda (o las modas) y la mediana y - ¿porqué no? - también se señalen los cuartiles para visualizar mejor el grado de dispersión. Sería interesante también que con esta gráfica se pudiesen comparar fácilmente diferentes poblaciones o grupos de una variable ordinal, para verificar cambios en la tendencia central de un grupo a otro. Si bien existen las gráficas de cajas comparativas, en las cuales las hendiduras indican posibles diferencias significativas entre las medianas de unos u otros subgrupos, la gráfica de caja (o boxplot) no es a mi criterio la más adecuada cuando las variables ordinales tienen pocos niveles (o categorías ordinales). Además, con las gráficas de cajas no podemos visualizar la moda o la distribución de frecuencias de la variable en las categorías ordinales.

Para poner las cosas en perspectiva, en la discusión que sigue voy a considerar un estudio sobre el rendimiento académico de jóvenes noruegos entre 13 y 15 años de edad y el nivel de ingresos familiar [Ver Hassan(2007)]. En este estudio, se consideraron dos grupos: uno llamado "grupo control", representado por una muestra de estudiantes sin distinción del nivel de ingresos familiar y otro grupo - el "grupo caso" - representado por una muestra de estudiantes provenientes de hogares con un ingreso agregado ubicado en el 60% o menos del ingreso familiar mediano en Noruega. Se consideraron las notas de estos estudiantes para tres áreas claves: Matemáticas, Inglés y Noruego. Como en Noruega las notas son de la escala entre 1 y 6, siendo el "6" la nota más alta, la variable asociada al rendimiento académico en cada área es en efecto una variable ordinal. Las distribuciones de las notas (en porcentajes) correspondientes a los subgrupos "caso" y "control" para las tres áreas de conocimiento respectivas son dadas según la siguiente tabla:

Matemática				Inglés				Noruego
Caso		Control		Caso		Control		Caso		Control
Nota	Frec	Nota	Frec	Nota	Frec	Nota	Frec	Nota	Frec	Nota	Frec
1	1%	1	1%	1	1%	1	0%	1	0%	1	0%
2	16%	2	5%	2	8%	2	5%	2	5%	2	3%
3	30%	3	26%	3	25%	3	21%	3	25%	3	24%
4	31%	4	43%	4	40%	4	43%	4	46%	4	45%
5	19%	5	22%	5	24%	5	27%	5	24%	5	26%
6	3%	6	3%	6	2%	6	4%	6	0%	6	2%

¿Cómo podríamos comparar los subgrupos de "caso" y "control" a través de las tres áreas de conocimiento mediante una gráfica? Si hiciéramos múltiples gráficas de barras, se vería como en la gráfica a la derecha.

¿Sirve éste resumen gráfico a los fines comparativos de detectar diferencias entre el rendimiento académico de estudiantes de bajos ingresos familiares y la población estudiantil en general?

Para las tres áreas académicas, la calificación modal de un grupo y otro es "4", por lo cual no se pueden detectar diferencias entre uno y otro subgrupo si solamente se toma en cuenta la moda. Más sin embargo, en el caso de la asignatura de matemáticas, se observa cierto desplazamiento hacia las calificaciones más bajas para el subgrupo de estudiantes con menores ingresos familiares.

Cómo los diagramas de barras de arriba no incluyen otros indicadores de tendencia central o de posición, es difícil establecer comparaciones más precisas. Además, un buen resumen gráfico de esta data debería de permitir constatar "desplazamientos" entre las calificaciones de un grupo y de otro.

Con esta idea de visualizar los "desplazamientos de las calificaciones" me puse a buscar sobre técnicas gráficas alternativas y di con un artículo en el cual el autor elaboraba sobre un tipo de gráficas llamada "gráficas de barras apiladas divergentes". En este tipo de gráficas, se empatan barras horizontales cuya longitud es proporcional a la frecuencias de los niveles consecutivos de la variable ordinal para cada subgrupo poblacional, formando una sola barra horizontal para cada subgrupo respectivo con varias barras apiladas de izquierda a derecha. Estas barras horizontales compuestas de varias barras apiladas se desplazan de modo que el punto cero se ubique en el medio de la clase central de la escala ordinal (para el caso en que el número de clases de la escala sea un número impar) o entre las dos clases del medio si el número de clases es par. De este modo, cuando colocamos las barras horizontales de cada subgrupo una encima de la otra de tal manera que todos los puntos "cero" estén alineados en una recta vertical, podemos constatar visualmente los desplazamientos entre uno y otro subgrupo.

Adicionalmente, pensé que sería buena idea sombrear las barras apiladas de cada barra horizontal de modo que los tonos más oscuros se correspondiesen a las frecuencias de clase mas altas. Además, si indicamos la posición del 1er, 2ndo y 3er cuartíl en cada barra sería de mucha utilidad para visualizar las medidas de posición y así hacerlas conmensurables con los desplazamientos. Preparé un pequeño script en R para elaborar esas gráficas, que pueden ver a continuación:

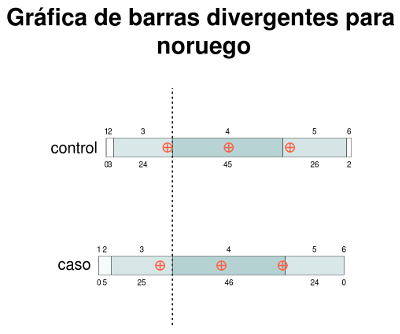
Las gráficas de arriba permiten una mejor comparación del rendimiento académico de los estudiantes de bajos ingresos familiares y aquel de la población estudiantíl en general. Para el caso de la asignatura de "Noruego" (lengua primaria), no se observan diferencias importantes entre las calificaciones de uno y otro grupo. Para el caso de "Inglés" (lengua secundaria) se observa un leve desplazamiento hacia las calificaciones más bajas de parte del grupo de estudiantes de bajos ingresos familiares (identificado como "caso"). Para matemáticas, se observa un desplazamiento más acentuado, en donde los estudiantes de bajos ingresos obtuvieron calificaciones más bajas. Obsérvese que la barra horizontal de este grupo está más desplazada hacia la izquierda.

Coloco el código R abajo en este post para quien esté interesado. Quizás incorpore este tipo de gráficas en mi librería estUNA, pero todavía lo considero en etapa experimental.

#la data es tomada del estudio en "3827_1.pdf"

matematicas <- data.frame (caso    = c(0.01,0.16,0.30,0.31,0.19,0.03),

                           control = c(0.01,0.05,0.26,0.43,0.22,0.03) )

ingles <- data.frame(caso    = c(0.01,0.08,0.25,0.40,0.24,0.02),

                     control = c(0.00,0.05,0.21,0.43,0.27,0.04) )

noruego <- data.frame(caso    = c(0.00,0.05,0.25,0.46,0.24,0.00),

                      control = c(0.00,0.03,0.24,0.45,0.26,0.02) )

graficar_barras_divergentes <- function(mdata,nombre=deparse(substitute(mdata))) {

  #esta función supone que mdata es un marco de datos

  #en donde cada columna se asocia a los porcentajes de los niveles

  #de una escala ordinal en orden ascendente (ie. el primer elemento del

  #vector se corresponde a la frecuencia del menor nivel en la escala).

  mdata_ac <- rbind(mdata,rep(0,ncol(mdata)))

  filas_par <- (nrow(mdata) %% 2 == 0)

  for (i in 1:ncol(mdata)) {

    x <- cumsum(mdata[[i]])

    if (filas_par)

      mid <- x[nrow(mdata) %/% 2]

    else

      mid <- x[nrow(mdata) %/% 2] + mdata[[i]][(nrow(mdata) %/% 2) + 1]/2

    mdata_ac[[i]] <- c(-mid,x -mid)

  }

  #crea un nuevo cuadro del tamaño adecuado

  frame()

  plot.window(xlim=c(min(mdata_ac)-0.2,max(mdata_ac)),ylim=c(0,0.5*ncol(mdata_ac)))

  #dibuja una línea vertical punteada de "centralidad"

  lines(c(0,0),c(0,0.5*ncol(mdata_ac)),lty="dotted")

  for (i in 1:ncol(mdata_ac) ) {

    #calcula la posición de las etiquetas para las frecuecias/categorias

    lbx <- (tail(mdata_ac[[i]],-1)+head(mdata_ac[[i]],-1))/2

    #dibuja los rectángulos que componen las frecuencias de cada clase

    for (j in 1:(nrow(mdata_ac)-1) )

      rect(mdata_ac[j,i], 0.21 + (i-1)*0.5 ,mdata_ac[j+1,i], 0.29 + (i-1)*0.5 ,

               col=rgb(95/256,158/256,160/256,alpha=mdata[j,i]) , lwd=0.25 )

    #escribe las frecuencias

      text(x=lbx,y=0.18+(i-1)*0.5,cex=0.4,labels=round(mdata[[i]]*100,digits=2) )

    #escribe las etiquetas de categorías

      text(x=lbx, y=0.32+(i-1)*0.5,cex=0.4,labels=rownames(mdata) )

    #indica los cuartiles

    #indica cuartiles

      points(seq(from=0.25,to=0.75,by=0.25)+mdata_ac[1,i],rep(0.25+(i-1)*0.5,3),col="tomato",pch=10)

  }

  #escribe las etiquetas de cada serie de datos

  text(x=min(mdata_ac)-0.1,y=seq(from=0.25,to=0.25+0.5*ncol(mdata),by=0.5),cex=0.8,labels=colnames(mdata) )

  #El titulo

  title(main=paste("Gráfica de barras divergentes para\n",nombre) )

}

ppi <- 300

png("gbd%2d.png",width=ppi*4,height=ppi*4,res=ppi)

graficar_barras_divergentes(matematicas)

graficar_barras_divergentes(ingles)

graficar_barras_divergentes(noruego)

graphics.off()

png("graficos_de_barras.png",width=ppi*4,height=ppi*6,res=ppi)

par(mfrow=c(3,2))

barplot(matematicas[[1]],names.arg=1:6,main="Matematicas",sub="(grupo caso)")

barplot(matematicas[[2]],names.arg=1:6,main="Matematicas",sub="(grupo control)")

barplot(ingles[[1]],names.arg=1:6,main="Ingles",sub="(grupo caso)")

barplot(ingles[[2]],names.arg=1:6,main="Ingles",sub="(grupo control)")

barplot(noruego[[1]],names.arg=1:6,main="Noruego",sub="(grupo caso)")

barplot(noruego[[2]],names.arg=1:6,main="Noruego",sub="(grupo control)")

graphics.off()

Bibliografía

HASSAN, J. (2007). Parents’ socioeconomic status and children’s academic performance. Norwegian Social Research. NOVA Notat 7/2009.
HEIBERGER, R. y ROBBINS, N. (2011). Plotting Likert and Other Rating Scales Section on Survey Research Methods – JSM 2011.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.