Trabajo práctico de la 745, lapso 2016-1

Como seguramente ustedes saben, los trabajos prácticos de estadística pasaron a ser evaluaciones formativas desde hace algunos semestres. A partir de entonces, el objetivo 1 de Estadística General (745) se evalúa en la primera parcial y en la integral. Aunque ya no es necesario entregar un trabajo práctico cómo tal ni recibirá una calificación departe mía, yo les recomendaría realizar las actividades contempladas en el enunciado del trabajo, que fueron publicadas aqui. La razón de mi recomendación es porque en este semestre, las actividades del trabajo práctico contemplan la elaboración de diagramas de caja y de torta. Mi olfato docente me obliga a avisarles sobre esto e invitarlos a que continúen leyendo esta entrada, donde realizaremos juntos las actividades propuestas, no vaya a ser que las gráficas de tortas y de caja los agarren desprevenidos este semestre...

Trabajos de Estadística (738/748, 745 y 746) Lapso 2016-1

Se ha publicado los enunciados para los trabajos prácticos de las siguientes materias: 738/748, 745 y 746. Ante todo permítanme aclararles que estos trabajos prácticos son actividades de evaluación formativa y como tal, no tienen fecha de entrega ni ponderación en la calificación final de la materia. Aún así, les recomiendo revisar los enunciados e intentar realizar las actividades que allí se piden. Los enlaces a las carpetas comprimidas con la data y los enunciados en ciberesquina se dan a continuación:

738/748

745

746

Trataré en próximas entradas de abordar las actividades contempladas en esos trabajos. Por los momentos, les recuerdo que pueden utilizar el lenguaje R para realizar las actividades ustedes mismos. En una página fija de este blog se da información para aquellos interesados en usar R. En este mismo blog he publicado video tutoriales sobre cómo instalar R y la librería estUNA así como un ejemplo del empleo de técnicas de estadística descriptiva. También encontrarán muchas entradas ilustrando distintos métodos de estadística en este programa.

Para este semestre, la data se encuentra en el siguiente data frame de estUNA: d20161

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

Técnicas de visualización de datos a ser utilizadas este semestre

En este lapso académico se les pide a los estudiantes de Estadística General (745) realizar diagramas de tallo y hoja, ojivas de frecuencia y diagramas de caja como parte de las actividades prácticas del objetivo 1. En esta entrada, hablaré un poco sobre estas técnicas de visualización de datos y como se implementan en R / estUNA.

Estadística General, Aplicada e Inferencial: Nuevos planes de evaluación y Trabajos Prácticos

Se le informa a los estudiantes inscritos en Estadística General (745), Estadística Aplicada (746) e Inferencia Estadística (738-748) que los planes de evaluación de estas materias han sido modificados para el semestre entrante 2014-1.  Donde antiguamente el objetivo 1 (745), el objetivo 6 (746) y los objetivos 8, 9 y 10 (738/748) eran evaluados mediante la elaboración de un informe cuya entrega era obligatoria, este semestre estos objetivos serán evaluados en la primera parcial (745), segunda parcial (746) y tercera parcial (738/748).  Los trabajos de estas materias son evaluaciones de tipo formativa, lo cual significa que deben ser realizadas por el estudiante, pero no se requiere la entrega de un informe o trabajo al asesor y por eso verán que en los enunciados no hay fechas de entrega, ni para el borrador ni para la versión final del informe.  Sin embargo, es importante que el estudiante realice el trabajo (pueden reunirse en grupos de estudio y con el asesor si requiere asesoría), debido a que las preguntas en los parciales se referirán a la interpretación de los resultados obtenidos tras realizar las actividades indicadas en el enunciado del trabajo.

Seguidamente les indico los enlaces de descarga de los enunciados:

• Trabajo práctico 745, 2014-1
• Trabajo práctico 746, 2014-1
• Trabajo práctico 738/748, 2014-1

Se ha actualizado la librería estUNA para incluir la data del semestre 2014-1. Pulse el enlace para descargar la librería. El dataframe para este semestre es d20141.  Próximamente, se estarán publicando entradas en este blog referente a la realización de algunas de las actividades prácticas de este semestre, como los diagramas de tallo y hoja, las ojivas, entre otras.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

Trabajo Práctico de Estadística 2013-2 - Bibliografía

En el trabajo práctico de estadística de este semestre (2013-2) se estudia una data relativa a la ceba de la cachama blanca. A tal fín incluyo algunas referencias bibliográficas al final de esta entrada.  Si alguien ha encontrado algunos recursos bibliográficos de interés, por favor indíquelos en los comentarios de esta entrada del blog.

Quisiera sugerirles que para la discusión/interpretación de los resultados tomen en cuenta la información básica sobre la piscicultura, que debe incluirse en el marco teorico de este informe.  La discusión/interpretación de los resultados es eso, no una mera repetición de los resultados. Por ejemplo, la moda de la variable X8 para datos sin agrupar es de 84,04, tal como lo reflejan en alguna tabla de los resultados. ¿Para qué repetir esto en la discusión de los resultados? Más bien, interpreten los resultados a la luz de los procedimientos y técnicas de este cultivo. Por ejemplo, ¿está la temperatura del agua o el Ph dentro del rango sugerido para el cultivo de la cachama blanca? Existe una regla para el suministro de alimento en la cual se toma en cuenta el cálculo de la biomasa (Número de alevines por peso promedio). ¿Concuerdan los datos con esta regla? Seguramente si leen un poco sobre el cultivo de la cachama, encontraran muchos otros elementos que les ayudarán a plantear una buena interpretación de los resultados.

Por último, les recuerdo que "Discusión de los resultados" no es lo mismo que "Conclusión". Básicamente, en la Conclusión ya no van a hacer referencia al cultivo de la cachama. Para más información ver este enlace en mi blog viejo.

Bibliografía

• TORRES, E. (2010). MANUAL DE PISCICULTURA DE AGUAS DULCES. Disponible en: http://www.alevinos-acuicultura.com/Portals/1/Manual%20Piscicultura%20Clientes.pdf .
• PEÑUELA-HERNANDEZ, Z., HERNÁNDEZ-AREVALO, G. , CORREDOR MATUS J. R., CRUZ-CASALLAS P. E.  (2007). Consumo de oxígeno en cachama blanca (Piaractus brachypomus) durante diferentes etapas de desarrollo corporal. Revista ORINOQUIA - Universidad de los Llanos. Vol. 11, N° 1. Disponible en: http://www.redalyc.org/pdf/896/89611105.pdf .
• GOMEZ-TRUJILLO, M. (2010). Manual de piscicultura para comunidades amazónicas. Instituto del Bien Común. Lima. Disponible en: http://www.sisman.utm.edu.ec/libros/FACULTAD%20DE%20CIENCIAS%20VETERINARIAS/CARRERA%20DE%20INGENIER%C3%8DA%20EN%20ACUICULTURA%20Y%20PESQUER%C3%8DAS/LIBROS%201/manual%20pisicultura.pdf.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

Estudio de estadística descriptiva en R /estUNA - video Tutorial

Video-tutorial sobre cómo utilizar el lenguaje R y la librería estUNA para realizar análisis exploratorio de datos como los que se piden en los trabajos prácticos de Estadística General (745):

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

Trabajos de Estadística para el 2013-2

Ya están disponibles los enunciados para los trabajos prácticos de estadística del semestre 2013-2, elaborados por Nivel Central.  Los enlaces se dan a continuación (según http://areamatematicas.galeon.com/):

• 745 - Estadística General
• 746 - Estadística Aplicada
• 738/748 - Inferencia Estadística
• Data en formato CSV
• Normas para la elaboración del informe

Sobre las fechas de entrega, se ha escrito en los enunciados lo siguiente:

La evaluación del trabajo comprende dos entregas obligatorias:

• 1era Entrega: primera versión del informe final entre el 09/11/2013 y el 16/11/2013, en esta oportunidad el trabajo será revisado por el asesor y el participante debe registrar las observaciones pertinentes a fin de realizar las correcciones, pues el trabajo lo retiene el asesor hasta la entrega final con el objeto de verificar que las correcciones fueron realizadas.
• 2da Entrega: Versión final del trabajo entre el 11/01/2014 y el 18/01/2014 improrrogable. De no respetar las dos entregas en los lapsos correspondientes queda a discreción del asesor considerar reprobado el trabajo.

 Nota: Me pueden enviar los trabajos (borrador y versión final) en formato Word 2003 o preferiblemente en Libre Office a mi correo: jlaurentum@gmail.com. Por favor no enviar en formato Word 2007 o posterior (extensión de archivo .docx). Ni siquiera abriré el archivo si se encuentra en este formato.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

Actualización de página tutorial de estUNA

Se ha actualizado la página tutorial de estUNA.  La librería también fue actualizada para ampliar algunas funcionalidades de la instrucción test.independencia, que se usa para el objetivo 8.2 de las asignaturas 738 y 748.  A continuación un esquema del contenido de la página tutorial:

1. Para comenzar a trabajar con la librería estUNA - enlace.
2. Estadística descriptiva para datos univariantes no agrupados (Objetivos 1 y 2 de la 745) - enlace.
3. Estadística descriptiva para datos univariantes agrupados (Objetivos 1 y 2 de la 745) - enlace.
4. Gráficas de dispersión y gráficas de caja comparativas - enlace.
5. Regresión lineal - enlace.
6. Contrastes de bondad de ajuste chi-cuadrado - enlace.
7. Tests de independencia chi-cuadrado - enlace.
8. Cómo enviar la salida gráfica a archivos - enlace.

Si necesitan alguna explicación sobre otros aspectos de la librería o tienen algún comentario sobre la página tutorial, pueden enviarme un correo a jlaurentum@gmail.com o dejar un mensaje en el buzón a la derecha de esta página.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

Taller - trabajos de las asignaturas de estadística

Hola:

Estoy anunciando un taller este próximo sábado (6/4/2013), a las 9:30am en la sede de la UNA en El Tigre con el siguiente contenido:

Elaboración de los trabajos prácticos de las asignaturas 745, 746 y 738/748.

Este taller estará enfocado en el uso del lenguaje R para abordar el aspecto computacional de los trabajos prácticos.  Se hará una breve inducción a la programación en R y se aplicará esta herramienta a la resolución de problemas similares a los del trabajo práctico.

Si va a asistir al taller y tiene computadora portátil, se recomienda  llevarla para practicar los ejercicios que desarrollaremos.  Si tiene cable de extensión, llévelo también.

Si tienen preguntas o aspectos que quieren que sean abordados en este próximo taller, por favor dejar sus comentarios abajo de esta entrada del blog.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

The Lending Club - parte III

En esta última entrada de la serie, procedemos a construir y analizar distintos modelos de regresión para descubrir cómo se determina la tasa de interés de los prestamos que se tramitan a través del Lending Club En entradas anteriores, dimos la información de contexto del problema bajo estudio (ver la primera parte) y luego realizamos un análisis exploratorio de datos (ver la segunda parte).

---

Primer modelo de regresión

Para comenzar, cargaremos el archivo de datos "lending_club.Rda" y la librería estUNA (el archivo tiene el mismo nombre), los cuales se supone que deben estar en el mismo directorio de trabajo. Seguidamente, nuestro script debe contener una instrucción attach para referirnos a las variables individuales del data-frame loandata de manera más sencilla.

load("estUNA")
load("lending_club.Rda")
attach(loandata)
options(width=60)
png("regresion%02d.png")

El primer modelo incluirá aquellas variables de loandata que consideramos significativas según el análisis exploratorio realizado en la entrada The Lending Club - parte II. Estas variables son:

• Ar (Monto Requerido).
• Fi (calificación FICO).
• Ld (Duración del prestamo)
• Ocl (Líneas de crédito abiertas)
• Inq0 (Variable indicadora según sea el número de indagaciones igual a 0).
• Lp_dc (Variable indicadora según sea el propósito del préstamo la consolidación de deudas).

Las últimas dos variables indicadoras, Inq0 y Lp_dc, no están definidas en loandata- hay que definirlas. Seguidamente se define el modelo de regresión como modelo1a y se imprime un resumen:

Lp_dc <- Lp=="debt_consolidation"
Inq0 <- Inq==0
modelo1a <- regresion.lineal(Ir~1+Ar+Fi+Ld+Inq0+Ocl+Lp_dc)
resumen(modelo1a)

--------------------------------------------------------------
Resumen de regresion lineal

  MODELO         : modelo1a 
  Marco de datos : variables globales 
  Formula        : Ir ~ 1 + Ar + Fi + Ld + Inq0 + Ocl + Lp_dc 

Estimacion de los coeficientes poblacionales

                Estimacion   Error Est. Estadistico T
[Intercepto]  7.382562e-01 8.548541e-03     86.360488
Ar            1.481033e-06 5.975320e-08     24.785830
Fi           -8.772580e-04 1.189671e-05    -73.739512
Ld60          3.201605e-02 1.081372e-03     29.606863
Inq0TRUE     -1.079905e-02 8.222849e-04    -13.132985
Ocl          -5.018680e-04 9.328141e-05     -5.380150
Lp_dcTRUE    -2.028007e-03 8.385869e-04     -2.418362
                p-valor
[Intercepto] < 2.22e-16
Ar           < 2.22e-16
Fi           < 2.22e-16
Ld60         < 2.22e-16
Inq0TRUE     < 2.22e-16
Ocl           8.138e-08
Lp_dcTRUE      0.015662

Prueba F global

  Valor F : 1342.558   gl. num: 6   gl. den : 2485 
  p-valor : < 2.22e-16 

Coeficientes de determinacion

   R^2 : 0.7642392   R^2 ajustado : 0.76367 

Residuos

  Minimo  : -0.094555 
  Mediana : -0.002316511 
  Maximo  : 0.09745238 

  Desv. estandar residual:  0.02032266 

--------------------------------------------------------------

Todas las variables independientes de este modelo son significativas (con p-valores muy por debajo de 5%). El coeficiente de determinación \(R^2\) es un poco más de 76%, lo cual no está mal. ¿Es este el mejor modelo que podemos producir? ¿Hay algún problema en el modelo de regresión? Esta última pregunta la responderemos definitivamente al hacer un análisis de residuos.

Por ahora quiero llamar su atención a la estimación del coeficiente de la variable Lp_dc, que es igual a -0,0020287. Lp_dc es una variable lógica (TRUE o FALSE), lo cual equivale a decir que es una variable categórica.  Por la forma en que está definida la variable,  Lp_dc es igual a TRUE (verdadero) cuando el propósito del préstamo es la consolidación de deudas. Como vimos en el análisis exploratorio, los prestamos solicitados para la consolidación de deudas tienen una tasa de interés más alta (en promedio) que la tasa de interés promedio global. Por lo tanto, esperaríamos que el coeficiente de esa variable fuese positivo, pero según los resultados obtenidos, ¡es negativo!

La variable Lp_dc tiene lo que se conoce como un efecto supresor en el modelo de regresión donde la variable dependiente es la tasa de interés.  Esto ocurre porque una (o posiblemente varias) de las otras variables independientes están correlacionadas con la varaible Lp_dc y con la variable Ir.   Podemos construir modelos de regresión en los cuales probamos eliminar cada una de las otras variables una por una, hasta obtener un modelo de regresión en donde el coeficiente de Lp_dc sea positivo (como debería ser).  Tras un poco de ensayo y error, se descubrió que Lp_dc tiene un efecto supresor sobre Ir en conjunto con la variable Ar.  Para probar, construimos un modelo de regresión igual al anterior, pero sin la variable Ar:

modelo1b <- regresion.lineal(Ir~1+Fi+Ld+Inq0+Ocl+Lp_dc)
resumen(modelo1b)

---------------------------------------------------------
Resumen de regresion lineal

  MODELO         : modelo1b
  Marco de datos : variables globales
  Formula        : Ir ~ 1 + Fi + Ld + Inq0 + Ocl + Lp_dc

Estimacion de los coeficientes poblacionales

                Estimacion   Error Est. Estadistico T
:                   :            :            :
:                   :            :            :
Lp_dcTRUE     1.717800e-03 9.210058e-04     1.8651343
                 :
                 :
Coeficientes de determinacion

   R^2 : 0.7059548   R^2 ajustado : 0.7053634
       :
       :
  Desv. estandar residual:  0.02269156

No se imprime la tabla completa de resumen para ahorrar espacio. Lo que se quiere resaltar es que para este modelo, el coeficiente de Lp_dcTRUE (prestamos cuyo propósito es la consolidación de deudas) es positivo, lo cual coincide con lo observado en el análisis exploratorio respecto a que los prestamos para consolidación de deudas tienen tasas de interés más altas.  Sin embargo, eliminamos una variable que era muy significativa (la variable Ar) y por lo tanto, el coeficiente de determinación disminuyó a un poco más de 70%- aproximadamente 6% menos que el modelo1a.  Para evitarnos el problema de tener una variable con efecto supresor, eliminaremos más bien la variable Lp_dc (que era menos significativa que Ar) e incorporaremos otra vez la variable Ar.  Una vez obtenido el nuevo modelo (modelo1c), imprimimos un resumen y generamos las gráficas para el diagnostico de residuos.

modelo1c <- regresion.lineal(Ir~1+Ar+Fi+Ld+Inq0+Ocl)
resumen(modelo1c)
graficar(modelo1c)

--------------------------------------------------------------
Resumen de regresion lineal

  MODELO         : modelo1c 
  Marco de datos : variables globales 
  Formula        : Ir ~ 1 + Ar + Fi + Ld + Inq0 + Ocl 

Estimacion de los coeficientes poblacionales

                Estimacion   Error Est. Estadistico T
[Intercepto]  7.349896e-01 8.449383e-03     86.987369
Ar            1.454991e-06 5.883215e-08     24.731215
Fi           -8.735828e-04 1.181075e-05    -73.965030
Ld60          3.206793e-02 1.082213e-03     29.631794
Inq0TRUE     -1.078765e-02 8.230728e-04    -13.106558
Ocl          -5.111106e-04 9.329393e-05     -5.478498
                p-valor
[Intercepto] < 2.22e-16
Ar           < 2.22e-16
Fi           < 2.22e-16
Ld60         < 2.22e-16
Inq0TRUE     < 2.22e-16
Ocl          4.7207e-08

Prueba F global

  Valor F : 1606.766   gl. num: 5   gl. den : 2486 
  p-valor : < 2.22e-16 

Coeficientes de determinacion

   R^2 : 0.7636844   R^2 ajustado : 0.7632091 

Residuos

  Minimo  : -0.09370228 
  Mediana : -0.002240513 
  Maximo  : 0.09816036 

  Desv. estandar residual:  0.02034247 

--------------------------------------------------------------

Verificamos que al volver a incorporar la variable Ar, el coeficiente de regresión sube a 76%. Realmente, la variable Lp_dc no contribuye en mucho sobre la variabilidad de la tasa de intereses. Para terminar de validar el modelo, estudiamos las gráficas de diagnóstico de análisis de residuos:

Fig 1.1	Fig 1.2
Fig 1.3

Las gráficas de verificación de normalidad (Fig. 1.1 y 1.2) no revelan desviaciones problemáticas de normalidad. Aún cuando el p-valor del test de normalidad revela que la distribución de los residuos es significativamente distinta de la distribución normal, podemos ver que en el plot cuantíl-cuantíl, ello se debe a que hay muchos residuos significativamente mayores a cero (son residuos atípicos).  Esto ocurre con frecuencia cuando tenemos tantos datos (2492 observaciones).  Lo que sí llama la atención son los patrones convexos (en forma de U) visibles en los diagramas de dispersión de los residuos versus las variables Fi y Ocl (Fig. 1.3.c y 1.3.d).  Esto revela que la relación entre estas variables y la tasa de interés (Ir) no es netamente lineal, lo cual ya habiamos advertido en el análisis exploratorio.  Tomando esta no linealidad en cuenta, incorporamos términos cuadráticos para estas variables, lo cual produce el modelo2:

---

Segundo modelo de regresión

modelo2 <- regresion.lineal(Ir~1+Ar+Fi+I(Fi^2)+Ld+Inq0+Ocl+I(Ocl^2))
resumen(modelo2)
graficar(modelo2)

Fig 2.1	Fig 2.2
Fig 2.3

En cuanto a la normalidad de los residuos, este segundo modelo es muy parecido al primero y valen las mismas observaciones que se hicieron anteriormente. Sin embargo, en las gráficas de dispersión de los residuos versus las variables independientes (Fig. 2.3) no se observa ningún problema de heterocedasticidad o no linealidad, por lo cual los residuos del segundo modelo tienen un "mejor" comportamiento que los del primer modelo. Ejecutando la instrucción resumen(modelo2) vemos la tabla de resumen:

--------------------------------------------------------------
Resumen de regresion lineal

  MODELO         : modelo2 
  Marco de datos : variables globales 
  Formula        : Ir ~ 1 + Ar + Fi + I(Fi^2) + Ld + Inq0 + Ocl + I(Ocl^2) 

Estimacion de los coeficientes poblacionales

                Estimacion   Error Est. Estadistico T
[Intercepto]  3.553545e+00 1.275557e-01      27.85877
Ar            1.558942e-06 5.216556e-08      29.88451
Fi           -8.637778e-03 3.535800e-04     -24.42949
Fi^2          5.366278e-06 2.444955e-07      21.94837
Ld60          3.218830e-02 9.567038e-04      33.64500
Inq0TRUE     -1.043817e-02 7.277374e-04     -14.34332
Ocl          -4.370420e-03 2.763538e-04     -15.81458
Ocl^2         1.597878e-04 1.087364e-05      14.69497
                p-valor
[Intercepto] < 2.22e-16
Ar           < 2.22e-16
Fi           < 2.22e-16
Fi^2         < 2.22e-16
Ld60         < 2.22e-16
Inq0TRUE     < 2.22e-16
Ocl          < 2.22e-16
Ocl^2        < 2.22e-16

Prueba F global

  Valor F : 1568.202   gl. num: 7   gl. den : 2484 
  p-valor : < 2.22e-16 

Coeficientes de determinacion

   R^2 : 0.8154726   R^2 ajustado : 0.8149526 

Residuos

  Minimo  : -0.09329256 
  Mediana : -0.001115824 
  Maximo  : 0.1044033 

  Desv. estandar residual:  0.01798302 

--------------------------------------------------------------

No solamente aumentó el coeficiente de determinación \(R^2\) de 76% a 81%, sino que la desviación estándar residual disminuyó de 0,0203 a 0,01798.  Esto último implica que los errores del modelo 2 son algo menores que los errores del modelo 1c, además de que las variables independientes del segundo modelo (con los términos cuadráticos de Fi y Ocl), explican un mayor porcentaje de la variabilidad de la tasa de interés que las del modelo 1c.

Hasta aquí deberíamos de estar bastante satisfechos con el modelo de regresión obtenido hasta ahora.  Podemos interpretar el significado de los coeficientes en el marco del problema original de la data del Lending Club.  Debido a que los coeficientes de del monto solicitado (Ar) y de la variable indicadora de prestamos de largo plazo (Ld60) son positivos, tenemos que la tasa de interés será mayor para prestamos de mayor monto requerido o mayor plazo.  El coeficiente de la variable indicadora Inq0TRUE es negativo, lo cual significa que aquellos prestamos para los cuales no se hicieron indagaciones (0 indagaciones) eventualmente tendrán una tasa de interés menor.  Las asociación entre la calificación FICO y la tasa de interés es algo más difícil de explicar, debido a la inclusión del término cuadrático.  De hecho, expresando la asociación de la tasa de interés con la puntuación FICO únicamente en términos de esta última, tenemos:

\[Ir \sim 3,55 - 0,00863\cdot Fi + 0,0000054\cdot Fi^2\]

Al graficar la curva de la fórmula anterior, tendríamos una parábola convexa en forma de U.  Esto quiere decir que para cierto rango de puntuación FICO, la tasa de interés desciende.  Alcanza un punto mínimo y luego comenzaría a ascender.  Si derivamos la función anterior respecto a la variable Fi e igualamos a cero, tenemos una tasa de interés mínima para una calificación FICO de aproximadamente 800 puntos, según este modelo.  Como la curva anterior es una parábola convexa, tendríamos que según este modelo, la tasa de interés comienza a ascender nuevamente para calificaciones FICO mayores de 800 puntos.  Claramente, esto no se corresponde del todo bien al tipo de asociación que esperaríamos entre ambas variables: un solicitante con una calificación FICO de 800 no debería obtener un crédito con menor tasa de interés que alguien con una calificación FICO de 850, porque este último tiene un mejor historial crediticio.  Sin embargo, no hay muchos prestamos con calificaciones FICO mayores a 800 puntos, y la rata de crecimiento en las tasas de intereses para estos casos no es tan significante.

Por último, vamos a hacer un experimento: construir un modelo de regresión igual al anterior pero sin un término de intercepto.  No es que esto sea una buena idea; de hecho, no lo es porque el termino del intercepto es muy significativo en el modelo 2 (p-valor casi nulo). Sin embargo, se quiere discutir un punto importante referente a la interpretación del coeficiente de determinación:

modelo3 <- regresion.lineal(Ir~-1+Ar+Fi+I(Fi^2)+
           Ld+Inq0+Ocl+I(Ocl^2))

                      :
                      :
                      :
Coeficientes de determinacion

   R^2 : 0.9828925   R^2 ajustado : 0.9828374

Residuos

  Minimo  : -0.09329256
  Mediana : -0.001115824
  Maximo  : 0.1044033

  Desv. estandar residual:  0.01798302

Pudiesemos pensar que estamos frente a un mejor modelo, con un coeficiente de determinación de 98% bastante superior al coeficiente de determinación del modelo de regresión anterior de 81%.  Sin embargo, si comparamos ambos modelos en base al error (medido en términos de la desviación estándar de los residuales), ambos modelos son semejantes, con una desviación estándar residual de 0,01798.  Examinando este asunto más minuciosamente y teniendo en cuenta que el coeficiente de determinación indica el porcentaje de variabilidad de la tasa de interés (variable dependiente) debido a la variabilidad de las variables independientes, debemos concluir que este coeficiente de determinación de 98% no revela lo que realmente está ocurriendo.  Es exagerado porque cuando no hay término de intercepto, una mayor cantidad de variabilidad de la variable dependiente será adosada a las variables independientes que quedan, de ahí que \(R^2\) se "infla" en tal magnitud al eliminar el término de intercepto de un modelo.

Del experimento anterior intuimos que la decisión de no incluir el término de intercepto no debe ser tomada a la ligera, solamente tomando en cuenta la ganancia en el coeficiente de determinación.  El termino de intercepto nos indica el valor de la variable dependiente cuando todas las variables independientes son iguales a cero.  Sin un término de intercepto, la tasa de interés sería cero cuando todas las variables independientes son iguales a cero, lo cual es absurdo.  Es preferible por lo tanto siempre incluir un término de intercepto porque este permite una mayor flexibilidad en la modelización de una variable, sobre todo si no conocemos muy bien sobre el marco teórico de aquello que intentamos modelar.  No incluir un término de intercepto en el modelo podría sesgar los valores ajustados de la variable dependiente- en la mayoría de los casos ocurre así. 

No obstante, existen situaciones, sobre todo en el campo de la economía, en donde si tiene sentido omitir el término de intercepto en una regresión.  Por ejemplo, el módelo de producción de Cobb-Douglas plantea la siguiente relación entre la producción (Y), el capital (K) y la mano de obra (L): \(ln\,Y = \beta_1\,ln\,K\,+\,\beta_2\,ln\, L\).  Incluir un término constante en este modelo (el término de intercepto) implicaria una situación irreal en la que hay producción (distinta de cero) sin capital y sin mano de obra.

---

Conclusiones

Tras este ejercicio de regresión, una de las conclusiones más importantes es que la evaluación comparativa de dos modelos de regresión no se puede realizar exclusivamente en términos de cuál modelo tiene un coeficiente de determinación mayor.  Siempre, como he insistido en otras entradas de este blog, hay que revisar los residuos.  El análisis de residuos es el que revela si existen fallas estructurales en un modelo que en la mayoría de los casos, tienen el efecto de "inflar" el coeficiente de determinación, invalidándolo como una métrica única para evaluar modelos.  En este caso, fue a través del análisis de residuos que se detectó la necesidad de incluir algún término de asociación no lineal de dos variables independientes importantes en el modelo.  La desviación típica de los errores es otro de los parámetros a tener en cuenta para evaluar cuál de entre varios modelos predice los valores de la variable dependiente con menos error.  Otro factor que hay que vigilar es el de las variables de confusión.  La presencia de variables de confusión en un modelo puede afectar en formas no deseadas la estimación de los coeficientes del modelo.  Por último, la eliminación (omisión) del término de intercepto es algo que se debe hacer con cuidado y siempre cuando haya fundamentos teóricos de la situación bajo estudio que lo justifiquen.  En todo caso, eliminar el término del intercepto casi siempre hace que el coeficiente de determinación aumente, pero esto no debe tomarse como un indicativo que los modelos sin términos de intercepto sean mejores.

Como citar esta entrada

Romero, J. (Marzo, 2013). The Lending Club - parte III. [Entrada de blog]. Recuperado desde https://unamatematicaseltigre.blogspot.com/2013/04/the-lending-club-parte-iii.html.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

The Lending Club - Parte II

Para comenzar a trabajar con este ejemplo

En la primera parte de esta serie de entradas, se expuso la información de contexto sobre el problema del Lending Club. En la siguiente parte, se hará el ejercicio de construcción de modelos de regresión lineal.

La data con la que se trabajará para este ejemplo está disponible para su descarga desde este enlace. Una vez descargado ese archivo, colóquelo en su directorio de trabajo de R, que usualmente será "Mis Documentos" en el caso de Windows. Para trabajar con este ejemplo, también debe tener la librería "estUNA" en su directorio de trabajo (consulte esta en si tiene dudas sobre cómo descargar estUNA y colocarla en su directorio de trabajo).

Sobre la data del problema del "Lending Club"

El archivo identificado arriba "lending_club.Rda" contiene un data frame identificado como loandata.  A continuación se detallan las variables contenidas en loandata como columnas.

Identificador de variable	Descripción
Ar	(Amount Requested) Monto solicitador por el prestatario para financiamiento.
Af	(Amount Funded) Monto financiado.
Ir	(Interest Rate) Tasa de Interés del financiamiento. Esta es la variable dependiente.
Ld	(Loan Duration) Variable categórica correspondiente a la duración del préstamo (36 o 60 meses).
Lp	(Loan Purpose) Variable categórica correspondiente al propósito del préstamo.
DtIR	(Debt-to-income Ratio) Coeficiente de deuda sobre ingresos.
St	(State) Código de dos letras correspondiente al estado de residencia del prestatario.
Ho	(Home ownership) Tipo de propiedad sobre la casa: "NONE" es ninguna casa, "MORTGAGE" indica hipoteca sobre la casa, "OWN" indica que la casa es propia y "RENT" indica que la casa es alquilada.
I	(Income) Ingreso mensual.
Fi	(FICO) Puntuación FICO del solicitante.
Ocl	(Open Credit Lines) Cantidad de líneas de crédito abiertas del solicitante.
Rcb	(Rotating credit balance) Balance rotativo de credito.
Inq	(Inquiries) Número de veces que algún comercio ha solicitado un reporte crediticio certificado.
Ed	(Employment duration) Tiempo en el actual empleo.

En todo informe de análisis de datos, es importante indicar el tamaño de la muestra empleada en el estudio.  El data frame loandata consta de 2492 observaciones (o renglones) y 14 variables (o columnas).

Análisis exploratorio de los datos

Antes de emprender el planteamiento de los modelos de regresión para inferir cuales variables, en definitiva, inciden sobre la fijación de la tasa de interés de un préstamo, es conveniente realizar un análisis exploratorio de los datos. En un análisis exploratorio se utilizan técnicas de la estadística descriptiva para "descubrir" el comportamiento de las variables, su variabilidad inherente y la variabilidad conjunta entre las mismas.El análisis exploratorio nos debe conducir a plantear uno o varios modelos de regresión viables y a entender cómo o donde estos pueden fallar.

A continuación damos el script en R que realiza los distintos pasos del análisis exploratorio. Si va a experimentar con este script en su computadora, recuerde que debe tener el archivo de la librería estUNA y el archivo de data lending_club.Rda en su directorio de trabajo. Seguidamente iremos interpretando los resultados.

load("estUNA")
load("lending_club.Rda")
attach(loandata)
options(width=60)
png("exploratorio%02d.png")
#Imprime un resúmen del data frame
summary(loandata)
#Matriz de correlación entre las variables cuantitativas
cor(loandata[,c("Ar","Af","Fi","I","Ocl","Rcb","Inq","Ir")])
#La primera gráfica es un histograma de Ir
graficar(Ir)
#A continuación unas graficas de dispersión
#Grafica la tasa de intereses (eje Y) versus:
graficar.dispersion(Ar,Ir,cex=0.2,pch=19)
#Monto solicitado
graficar.dispersion(Af,Ir,cex=0.2,pch=19)
#Monto financiado
graficar.dispersion(Fi,Ir,cex=0.2,pch=19)
#Puntuación FICO
graficar.dispersion(I,Ir,cex=0.2,pch=19)
#Ingreso mensual
graficar.dispersion(Ocl,Ir,cex=0.2,pch=19)
#Lin. credito abiertas
graficar.dispersion(DtIR,Ir,cex=0.2,pch=19)
#Deuda/Ingresos
graficar.dispersion(Rcb,Ir,cex=0.2,pch=19)
#Balance crédito rotativo
graficar.dispersion(Inq,Ir,cex=0.2,pch=19)
#Cantidad de indagaciones
#Diagramas de caja comparativos
#Grafica la relación entre la tasa de interés
#y las siguientes variables categóricas:
caja(Ir,Ho)   #Propiedad de la vivienda
caja(Ir,Ed)   #Tiempo en el empleo actual
caja(Ir,Ld)   #Plazo de financiamiento (36 o 60 meses)
#Para las siguientes dos variables, la visualización
#más adecuada es una tabla.
#Estudia la variabilidad de las tasas de interés según:
#1) El propósito del prestamo (Lp)
lp_mat <- t(sapply(levels(Lp),
            function(s)
               c(sum(Lp==s), median(Ir[Lp==s]),
                 wilcox.test(Ir~Lp==s)\(\$\)p.value)
              )
            )
colnames(lp_mat) <- c("frec","mediana","p_valor")
lp_mat <- as.data.frame(lp_mat)
lp_mat <- lp_mat[order(lp_mat\(\$\)frec,decreasing=TRUE),]
lp_mat
#2) El estado de residencia del prestatario:
st_mat <- t(sapply(levels(St),
            function(s)
               c(sum(St==s), median(Ir[St==s]),
                 wilcox.test(Ir~St==s)\(\$\)p.value)
              )
            )
colnames(st_mat) <- c("frec","mediana","p_valor")
st_mat <- as.data.frame(st_mat)
st_mat <- st_mat[order(st_mat\(\$\)frec,decreasing=TRUE),]
st_mat

Como primer paso del análisis exploratorio, se genera un resumen con las principales estadísticas del data frame. Esto lo hace la instrucción summary(loandata), tras lo cual se imprime lo siguiente:

       Ar              Af              Ir          Ld      
 Min.   : 1000   Min.   :  200   Min.   :0.0542   36:1944  
 1st Qu.: 6000   1st Qu.: 6000   1st Qu.:0.1016   60: 548  
 Median :10000   Median :10000   Median :0.1311            
 Mean   :12431   Mean   :12038   Mean   :0.1308            
 3rd Qu.:17000   3rd Qu.:16000   3rd Qu.:0.1580            
 Max.   :35000   Max.   :35000   Max.   :0.2489            
                                                           
                  Lp            DtIR              St      
 debt_consolidation:1306   Min.   :0.0000   CA     : 432  
 credit_card       : 442   1st Qu.:0.0975   NY     : 253  
 other             : 197   Median :0.1533   TX     : 174  
 home_improvement  : 152   Mean   :0.1540   FL     : 169  
 major_purchase    : 101   3rd Qu.:0.2068   IL     : 101  
 small_business    :  87   Max.   :0.3491   GA     :  97  
 (Other)           : 207                    (Other):1266  
        Ho             I                  Fi       
 MORTGAGE:1146   Min.   :   588.5   Min.   :642.5  
 NONE    :   0   1st Qu.:  3500.0   1st Qu.:682.5  
 OTHER   :   5   Median :  5000.0   Median :702.5  
 OWN     : 200   Mean   :  5687.6   Mean   :708.4  
 RENT    :1141   3rd Qu.:  6800.0   3rd Qu.:727.5  
                 Max.   :102750.0   Max.   :832.5  
                                                   
      Ocl             Rcb              Inq        
 Min.   : 2.00   Min.   :     0   Min.   :0.0000  
 1st Qu.: 7.00   1st Qu.:  5612   1st Qu.:0.0000  
 Median : 9.00   Median : 10978   Median :0.0000  
 Mean   :10.07   Mean   : 15263   Mean   :0.9013  
 3rd Qu.:13.00   3rd Qu.: 18900   3rd Qu.:1.0000  
 Max.   :38.00   Max.   :270800   Max.   :9.0000  
                                                  
       Ed     
 10+    :653  
 < 1    :247  
 2      :244  
 3      :234  
 5      :201  
 4      :192  
 (Other):721

Para las variables cuantitativas, la instrucción summary(...) devuelve una tabla con las principales medidas de posición (mínimo, 1er cuartíl, mediana y media, 3er cuartíl, máximo). Para las variables categóricas (o variables tipo "factor", como se les conoce en R), summary(...) devuelve una tabla de frecuencias para algunos niveles de la variable (los más frecuentes). Estos resultados permiten apreciar rápidamente cuál rango de valores asume cada variable.  Por ejemplo, podemos observar que la distribución de la variable Ar, en términos de los estadísticos de posición más importantes, es bastante similar a la de la variable Af. Esto tiene bastante sentido, pues esperaríamos que el monto solicitado y el monto financiado sean muy parecidos, una vez aprobado el préstamo.  Nótese el uso de la instrucción attach(...) al principio del script para referirse fácilmente a las variables de loandata en lo sucesivo.

Otra tabla bastante útil en un análisis exploratorio es la tabla de las correlaciones entre las variables.  Esto por cierto sería muy útil para estudiar la colinealidad o multicolinealidad de las variables, según se exige para el trabajo de este semestre.  La instrucción cor(...) en R genera una matriz cuadrada de correlaciones entre todas las variables.  Como cada variable está perfectamente correlacionada consigo misma, los elementos de la diagonal son todos "1".  De hecho,  una correlación de "1" o "-1" indica una colinealidad perfecta entre dos variables.  Puede consultar más sobre esto en el artículo de wikipedia sobre correlación lineal.  La matriz de correlación sólo tiene sentido para variables cuantitativas del data frame, lo cual en este caso se determina por medio de la instrucción cor(loandata[,c("Ar","Af","Fi","I","Ocl","Rcb","Inq","Ir")]) :

              Ar          Af           Fi           I
Ar    1.00000000  0.97022602  0.083040383  0.39109060
Af    0.97022602  1.00000000  0.073791988  0.37468574
Fi    0.08304038  0.07379199  1.000000000  0.12355539
I     0.39109060  0.37468574  0.123555388  1.00000000
Ocl   0.19680145  0.18779714 -0.090039520  0.17180076
Rcb   0.29277055  0.26116166  0.003217914  0.35936379
Inq  -0.02721561 -0.06224654 -0.092828774  0.03398569
Ir    0.33141077  0.33627376 -0.709911785  0.01231114
DtIR  0.07985656  0.09177385 -0.217596139 -0.16376264
             Ocl         Rcb         Inq          Ir
Ar    0.19680145 0.292770550 -0.02721561  0.33141077
Af    0.18779714 0.261161657 -0.06224654  0.33627376
Fi   -0.09003952 0.003217914 -0.09282877 -0.70991178
I     0.17180076 0.359363787  0.03398569  0.01231114
Ocl   1.00000000 0.290582979  0.10790657  0.09109025
Rcb   0.29058298 1.000000000  0.01285580  0.06042262
Inq   0.10790657 0.012855801  1.00000000  0.16846322
Ir    0.09109025 0.060422621  0.16846322  1.00000000
DtIR  0.37172725 0.188286897  0.01126195  0.17143913
            DtIR
Ar    0.07985656
Af    0.09177385
Fi   -0.21759614
I    -0.16376264
Ocl   0.37172725
Rcb   0.18828690
Inq   0.01126195
Ir    0.17143913
DtIR  1.00000000

Por razones tipográficas de espacio, la matriz de correlación de arriba se dividió en tres segmentos: el primero con las primeras cuatro columnas de la matriz, el segundo en el renglón de abajo con las siguientes cuatro columnas de la matriz y la última columna de la matriz en el tercer renglón. Nótese que la correlación de cada variable consigo misma es "1". También se puede observar que las variables Ar y Af están muy correlacionadas (correlación mayor a 97%). Esto implica que incluir ambas variables en un mismo modelo de regresión lineal puede generar un problema de colinealidad o multicolinealidad (para más detalles, puede consultar la sección 14.4 del libro "Probabilidad y Estadística" de G. Canavos). Ya se había comentado anteriormente sobre la relación (semántica) entre ambas variables- en lo sucesivo consideraremos solamente a la variable Ar, porque el monto solicitado del financiamiento es la información previa necesaria para decidir el monto a financiar y la tasa de interés del crédito.  También podemos notar que la puntuación FICO (Fi) y la tasa de interés (Ir) tienen bastante correlación (-0.71).  Esto indica que la variable Fi es una buena candidata para incluirse en un modelo de regresión lineal con la tasa de interés como variable dependiente.  Además, el signo negativo de la correlación indica que el coeficiente de regresión para la variable Fi en el modelo lineal también debería ser negativo.

La puntuación FICO del solicitante está muy correlacionada con la tasa de interés del préstamo. Pero a su vez, como vimos en la primera parte de esta serie (The Lending Club - Parte I), muchas de las variables en este data frame son tomadas en cuenta para el cálculo de la calificación FICO. Entonces, por una parte esperaríamos cierta correlación entre esas variables y la calificación FICO. Si esas variables se incluyen en el modelo lineal, pudiésemos estar ante un problema de variables de confusión (confounder variables).  Las variables de confusión son aquellas que están correlacionadas con la variable dependiente y con alguna o algunas de las otras variables independientes del modelo. El problema que generan las variables de confusión es que a veces, sus efectos sobre la variable dependiente pueden ser exagerados. También puede ocurrir lo que se llama un efecto supresor. Puede consultar más sobre estos temas en este blog. Por nuestra parte, algunos de estos conceptos saldrán a relucir a medida que iremos ensayando distintos modelos de regresión lineal.

A continuación podemos observar algunas gráficas. La primera (Fig. 1) es un histograma de las tasas de interés:

Fig. 1 - Histograma de las tasas de interés

Esta variable tiene una distribución casi acampanada ... ¡Un momento! ¿Qué es ese segundo pico que se observa a la izquierda, en el intervalo [0,06 - 0,08)? Bueno, una variable así difícilmente sea normalmente distribuida, lo cual no es un problema en sí. Sin embargo, llama la atención que exista un grupo tan significativo de prestamos con tasas de interés en ese rango.  Quizás, alguna de las variables independientes pueda explicar ese comportamiento...

Seguimos con la parte más ilustrativa de nuestro análisis exploratorio, que son las gráficas de dispersión entre la tasa de interés y las otras variables cuantitativas (Fig. 2):

Fig. 2 - Gráficas de dispersión de las variables independientes cuantitativas respecto a la variable dependiente Ir.

(a) Ar / Ir	(b) Fi / Ir
(c) I / Ir	(d) Ocl / Ir
(e) DtIR / Ir	(f) Rcb / Ir
(g) Inq/ Ir

Los diagramas de dispersión de la Figura 2 confirman que, entre todas las variables independientes, la calificación FICO (Fi) es la más fuertemente asociada a la tasa de interés (Ir). Esto era de esperarse, pero el diagrama de dispersión de la Figura 2.b. revela más detalles sobre esta asociación: la curva lowess (la línea verde oscura) tiene la misma pendiente hasta una puntuación FICO de 750 (aproximadamente, o a pepa de ojo). A partir de 750 puntos en la calificación FICO, la pendiente de la curva lowess se hace más horizontal.  Esto implica que a mayor puntuación FICO, menor tasa de interés del préstamo, pero a partir de 750 puntos FICO, la diferencia no es tan grande.  Dado la magnitud de la asociación entre estas dos variables, la recta lineal quizás no sea el tipo de asociación más idónea entre estas variables.

Otro patron marcado según la curva lowess se puede observar (ver Figura 2.a) en la asociación del monto solicitado para el financiamiento (Ar) y la tasa de interés (Ir), aunque esta asociación no es tan marcada como la asociación Fi-Ir, cuyos puntos en el diagrama de dispersión son menos dispersos respecto a la curva lowess. También se observa una relación creciente entre la cantidad de líneas de crédito abiertas y la tasa de interés (Figura 2.d).   Esta asociación podría no ser no-lineal, dado la convexidad de la curva lowess que se observa en la gráfica.

La variable DtIr (relación Deuda-Ingresos) también tiene una asociación creciente con la tasa de interés (ver Figura 2.e). Sin embargo, dada la baja correlación entre estas variables (de apenas 0.17 según la matriz de correlación de arriba) y el alto grado de dispersión de los puntos, es posible que esta variable no sea significativa en un modelo de regresión.  La Figura 2.g revela un patrón interesante: para 0 indagaciones (solicitudes de reportes de historial crediticio), las tasas de interés son más bajas.  Para 1 o más indagaciones, las tasas de interés no difieren significativamente.  Esto indica que posiblemente sea conveniente transformar la variable Inq a una variable indicadora según sea Inq=0 o no.

Las otras dos variables, ingresos mensuales (I) y balance rotativo de crédito (Rcb) contienen muchos datos atípicos hacia el extremo derecho para ser útiles.  Estos datos atípicos (en forma de ingresos mensuales astronomicamente altos por ejemplo) podrían afectar la regresión en formas no deseadas, por lo cual su inclusión en un modelo de regresión quizás no sea una buena idea.

Para explorar la asociación entre la tasa de interés y otras variables categóricas, lo más conveniente es usar diagramas de caja comparativos. Así se hizo para las variables Ho, Ed y Ld, como se muestra en la Figura 3:

(a) Ir ~ Ho

(b) Ir ~ Ed

(c) Ir ~ Ld

Las primeras dos gráficas de caja (Figuras 3.a y 3.b) no revelan asociaciones significativas entre la tasa de interés y las respectivas variables. En contraste, La Figura 3.c indica que si hay una relación significativa entre la tasa de interés y la duración del préstamo: los prestamos de 36 meses tienen tasas de interés signficativamente más bajas.

Para las otras dos variables cualitativas - el estado de residencia (St) y el propósito del préstamo (Lp) - no se hicieron diagramas de caja comparativos porque estas variables tienen demasiados niveles (46 estados y 14 propósitos de préstamo diferentes).  Para cada una de estas variables, se optó por generar tablas indicando la frecuencia de cada nivel, la tasa de interés mediana y el p-valor del contraste Wilcoxon de diferencia entre medianas (consultar el artículo en Wikipedia). La idea es verificar si para algún nivel determinado de estas variables, las tasas de interés difieren significativamente de aquellas asociadas a los otros niveles. Para la variable estado (St):

   frec mediana    p_valor
CA  432 0.13110 0.69246237
NY  253 0.13110 0.82515314
TX  174 0.13110 0.30747046
FL  169 0.13110 0.88525055
IL  101 0.12530 0.22145716
GA   97 0.12180 0.27619025
PA   96 0.13045 0.23581778
NJ   92 0.12120 0.38675613
VA   78 0.12550 0.78497883
MA   73 0.12120 0.38183801
OH   71 0.12230 0.10542538
MD   68 0.13790 0.62463807
NC   64 0.12405 0.34075690
CO   61 0.13110 0.92712927
WA   58 0.13110 0.89902872
CT   50 0.13140 0.29789052
AZ   46 0.13110 0.86390489
MI   45 0.14090 0.01538049
MN   38 0.13545 0.34930242
:     :     :        :
:     :     :        :

Esta tabla (dada aquí de forma parcial) enumera los 46 estados en orden descendente por frecuencia de observaciones. Podemos observar que para el estado MI (Michigan), la tasa de interés mediana es significativamente distinta de la de los otros estados (con un p-valor de 1% en el contraste de Wilcoxon). Esto implica que los prestamos de los solicitantes de ese estado tienen una tasa de interés más alta, por alguna razón. Sin embargo, como solo 45 de las 2492 observaciones son de ese estado, incluir la variable St en un modelo de regresión lineal solamente para ajustar mejor a un grupo que representa menos del 2% de las observaciones sería un despropósito. Seguidamente tenemos una tabla similar para el propósito del prestamo: 

                   frec mediana      p_valor
debt_consolidation 1306 0.13490 6.704956e-11
credit_card         442 0.13110 9.769974e-01
other               197 0.13060 6.911076e-01
home_improvement    152 0.11130 2.162582e-06
major_purchase      101 0.11120 2.559098e-08
small_business       87 0.12840 6.169896e-01
car                  50 0.10475 9.231269e-04
wedding              39 0.12210 2.223396e-01
medical              30 0.13110 8.066417e-02
moving               29 0.13110 6.110691e-01
vacation             21 0.12120 3.160609e-01
house                20 0.13085 8.177116e-01
educational          14 0.09755 4.628680e-02
renewable_energy      4 0.09130 1.336665e-01

Para esta variable, si se observa un subgrupo grande (con 1306 observaciones), cuya tasa de interés difiere significativamente de la de otros grupos (p-valor casi nulo).  Este grupo es el grupo de prestatarios que solicitaron un préstamo para consolidación de deudas (debt consolidation). Existen otros grupos con tasas de interés significativamente distintas, pero son muy pequeños en relación con el número total de observaciones. Por cierto, la tasa de interés mediana de los prestamos solicitados para consolidación de deudas (13,49%) es mayor a la tasa de interés mediana general (13,11%). De esto se deduce que sería conveniente incluir una variable indicadora en el modelo de regresión según sea el propósito del préstamo la consolidación de deudas o no.

---

Análisis exploratorio de datos - algunas conclusiones

Tras realizar el ejercicio anterior, podemos concluir sobre la importancia de explorar los datos antes de construir los modelos de regresión. Las observaciones realizadas tras este estudio exploratorio se pueden aunar al conocimiento o a las ideas previas que tenemos sobre la temática que estamos estudiando (en este caso, los prestamos personales en EEUU). Esto ayudará a plantear posibles hipótesis sobre las relaciones de las variables en forma de modelos de regresión lineal. Es importante destacar que un análisis exploratorio no es inferencial. Todo lo que observamos hasta este punto queda en forma de conjetura y no es generalizable a la población. Cuando, tras realizar el ajuste por mínimos cuadrados de un modelo de regresión lineal, tenemos los p-valores de la prueba F, los estadísticos T-Student de significatividad de los coeficientes poblacionales y cuando finalmente realicemos un análisis de residuos para validar el modelo, si tendremos los elementos estadísticos requeridos para un estudio inferencial. El análisis exploratorio sirve para guiar al análisis de regresión, el cual haremos en la tercera y última parte de estas entradas del blog...

Como citar esta entrada

Romero, J. (Marzo, 2013). The Lending Club - parte II. [Entrada de blog]. Recuperado desde https://unamatematicaseltigre.blogspot.com/2013/03/the-lending-club-parte-ii.html.


Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

Trabajos de estadística para el semestre 2013-1

Ya están disponibles los enunciados para los trabajos prácticos de estadística del semestre 2013-1, elaborados por Nivel Central.  Los enlaces se dan a continuación (según http://areamatematicas.galeon.com/):

• 745 - Estadística General
• 746 - Estadística Aplicada
• 738/748 - Inferencia Estadística
• Data en Excel
• Normas para la elaboración del informe

Sobre las fechas de entrega, se ha escrito en los enunciados lo siguiente:

La evaluación del trabajo comprende dos entregas obligatorias:

• 1era Entrega: primera versión del informe final entre el 15/04/2013 y el 20/04/2013, en esta oportunidad el trabajo será revisado por el asesor y el participante debe registrar las observaciones pertinentes a fin de realizar las correcciones, pues el trabajo lo retiene el asesor hasta la entrega final con el objeto de verificar que las correcciones fueron realizadas.
• 2da Entrega: Versión final del trabajo entre el 20/05/2013 y el 25/05/2013
  improrrogable. De no respetar las dos entregas en los lapsos correspondientes queda a discreción del asesor considerar reprobado el trabajo.

Cómo de costumbre, las entregas se pueden hacer enviando a mi correo el informe en Open Office, PDF o Word (ojo, versión 2003, no enviar en versión 2007 o posterior).

Les recomiendo (aunque no es obligatorio) el uso de R para la elaboración de este trabajo.  La data para este semestre ya está incorporada en mi librería estUNA.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

Una pregunta de probabilidades

Si responde a esta pregunta de forma aleatoria, ¿cuál es la probabilidad de acertar la repuesta correcta?

1. 0%
2. 25%
3. 25%
4. 50%

Su respuesta en los comentarios...

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.

Consideraciones sobre la visualización de datos - parte 2

Continuamos con la serie de entradas sobre la visualización de datos, esta vez complementando un poco lo dicho sobre las gráficas de torta en la entrada pasada. ¿Cuándo deben o no usarse? ¿Cómo se deben usar?

En el semestre pasado 2012-1, la data del trabajo práctico versaba sobre un estudio de nutrición infantil donde se estudiaban varios factores conjuntamente como el Índice de Masa corporal, el peso, la estatura y la actividad física, entre otros. Para la asignatura de Estadística General (745), se requería, entre otras cosas, elaborar una gráfica de torta para la variable X7 - el índice de actividad física. A continuación muestro una típica gráfica de estas. Nótese que en el ejemplo de abajo, la gráfica de tortas es tridimensional, por lo cuál le hice observaciones al estudiante según las explicaciones en la entrada anterior. Para el trabajo final, los estudiantes re-elaboraron estas gráficas de torta en dos dimensiones, con lo cual dieron cumplimiento a la actividad correspondiente requerida en el enunciado del trabajo. Sin embargo - y con la presión del semestre ya dejada atrás, le invito a echar un segundo vistazo a esta gráfica. Aparte de la tridimensionalidad, ¿nota algún otro problema con esta gráfica?

Es necesario considerar el tipo de variable o la escala de X7. Si observa la leyenda a la derecha, verá que los niveles o valores del índice de actividad física son: sedentario, ligera, moderada, alta y muy alta. En efecto, la variable X7 se refiere a la intensidad o la frecuencia de actividad física de los individuos de la muestra. Podemos establecer comparaciones de orden entre estos niveles de actividad física. Por ejemplo, una persona con actividad moderada tiene menos actividad física que otra persona cuyo nivel de actividad es "alta". En resumen, X7 es una variable de escala ordinal. ¿Qué tiene esto que ver con las gráficas de torta?

En teoría, las gráficas de torta permiten visualizar el valor modal de una muestra. El valor modal es aquel con mayor frecuencia y por lo tanto el sector correspondiente en la gráfica de torta se verá más grande. Sin embargo, la variable X7 es una variable ordinal. Sus niveles tienen una jerarquía, un orden de menor a mayor. Gracias a ese orden jerárquico de sus niveles, la variable X7 tiene mediana, aparte de tener moda. Por cierto, la moda de esta variable es "actividad física alta" y su mediana es "actividad física moderada".

La gráfica de torta de arriba es deficiente. No logra comunicar toda la estructura jerárquica de orden que la variable X7 posee por ser una variable ordinal. En efecto, en una circunferencia no hay ningún punto privilegiado, no hay un cero natural, pues dejaría de serlo al rotar la circunferencia. Si uno recorre la circunferencia en cualquier dirección, regresa al punto de partida y por lo tanto en una circunferencia tampoco hay una dirección que esté asociada con "más de algo" o "menos de algo". Es decir, en una circunferencia no podemos reflejar ninguna jerarquía de orden. Si la gráfica de torta no es el tipo de gráfica más adecuada para resumir visualmente esta variable, ¿cuáles otros tipos de gráfica deberíamos de considerar?

La gráfica de barras es una alternativa natural para visualizar variables de escala ordinal cómo la variable X7. Si en el eje de las abscisas disponemos los niveles de X7 de menor a mayor (en la gráfica de arriba los niveles de actividad tienen una codificación numérica de 1.0 a 1.8) y hacemos corresponder los valores de las frecuencias en el eje de las ordenadas, las alturas de las barras encima de cada nivel de las abscisas nos permite visualizar la forma de la distribución de la variable X7. Aparte de poder visualizar la moda tal como en la gráfica de tortas, una gráfica de barras permite visualizar la asimetría, la dispersión y la forma general de la distribución de frecuencias, lo cual no podíamos hacer con una gráfica de tortas. Ampliando un poco más esta gráfica, podríamos por ejemplo señalar la clase mediana.

Sin embargo, sobre este último punto surge una inquietud respecto a si no existirá otro tipo de gráfica más "informativa" para variables de escala ordinal. Un tipo de gráfica que permita señalar la diferencia entre la moda (o las modas) y la mediana y - ¿porqué no? - también se señalen los cuartiles para visualizar mejor el grado de dispersión. Sería interesante también que con esta gráfica se pudiesen comparar fácilmente diferentes poblaciones o grupos de una variable ordinal, para verificar cambios en la tendencia central de un grupo a otro. Si bien existen las gráficas de cajas comparativas, en las cuales las hendiduras indican posibles diferencias significativas entre las medianas de unos u otros subgrupos, la gráfica de caja (o boxplot) no es a mi criterio la más adecuada cuando las variables ordinales tienen pocos niveles (o categorías ordinales). Además, con las gráficas de cajas no podemos visualizar la moda o la distribución de frecuencias de la variable en las categorías ordinales.

Para poner las cosas en perspectiva, en la discusión que sigue voy a considerar un estudio sobre el rendimiento académico de jóvenes noruegos entre 13 y 15 años de edad y el nivel de ingresos familiar [Ver Hassan(2007)]. En este estudio, se consideraron dos grupos: uno llamado "grupo control", representado por una muestra de estudiantes sin distinción del nivel de ingresos familiar y otro grupo - el "grupo caso" - representado por una muestra de estudiantes provenientes de hogares con un ingreso agregado ubicado en el 60% o menos del ingreso familiar mediano en Noruega. Se consideraron las notas de estos estudiantes para tres áreas claves: Matemáticas, Inglés y Noruego. Como en Noruega las notas son de la escala entre 1 y 6, siendo el "6" la nota más alta, la variable asociada al rendimiento académico en cada área es en efecto una variable ordinal. Las distribuciones de las notas (en porcentajes) correspondientes a los subgrupos "caso" y "control" para las tres áreas de conocimiento respectivas son dadas según la siguiente tabla:

Matemática				Inglés				Noruego
Caso		Control		Caso		Control		Caso		Control
Nota	Frec	Nota	Frec	Nota	Frec	Nota	Frec	Nota	Frec	Nota	Frec
1	1%	1	1%	1	1%	1	0%	1	0%	1	0%
2	16%	2	5%	2	8%	2	5%	2	5%	2	3%
3	30%	3	26%	3	25%	3	21%	3	25%	3	24%
4	31%	4	43%	4	40%	4	43%	4	46%	4	45%
5	19%	5	22%	5	24%	5	27%	5	24%	5	26%
6	3%	6	3%	6	2%	6	4%	6	0%	6	2%

¿Cómo podríamos comparar los subgrupos de "caso" y "control" a través de las tres áreas de conocimiento mediante una gráfica? Si hiciéramos múltiples gráficas de barras, se vería como en la gráfica a la derecha.

¿Sirve éste resumen gráfico a los fines comparativos  de detectar diferencias entre el rendimiento académico de estudiantes de bajos ingresos familiares y la población estudiantil en general? Para las tres áreas académicas, la calificación modal de un grupo y otro es "4", por lo cual no se pueden detectar diferencias entre uno y otro subgrupo si solamente se toma en cuenta la moda.  Más sin embargo, en el caso de la asignatura de matemáticas, se observa cierto desplazamiento hacia las calificaciones más bajas para el subgrupo de estudiantes con menores ingresos familiares.

Cómo los diagramas de barras de arriba no incluyen otros indicadores de tendencia central o de posición, es difícil establecer comparaciones más precisas. Además, un buen resumen gráfico de esta data debería de permitir constatar "desplazamientos" entre las calificaciones de un grupo y de otro.

Con esta idea de visualizar los "desplazamientos de las calificaciones"  me puse a buscar sobre técnicas gráficas alternativas y di con un artículo en el cual el autor elaboraba sobre un tipo de gráficas llamada "gráficas de barras apiladas divergentes".  En este tipo de gráficas, se empatan barras horizontales cuya longitud es proporcional a la frecuencias de los niveles consecutivos  de la variable ordinal para cada subgrupo poblacional, formando una sola barra horizontal para cada subgrupo respectivo con varias barras apiladas de izquierda a derecha.  Estas barras horizontales compuestas de varias barras apiladas se desplazan de modo que el punto cero se ubique en el medio de la clase central de la escala ordinal (para el caso en que el número de clases de la escala sea un número impar) o entre las dos clases del medio si el número de clases es par.  De este modo, cuando colocamos las barras horizontales de cada subgrupo una encima de la otra de tal manera que todos los puntos "cero" estén alineados en una recta vertical, podemos constatar visualmente los desplazamientos entre uno y otro subgrupo.

Adicionalmente, pensé que sería buena idea sombrear las barras apiladas de cada barra horizontal de modo que los tonos más oscuros se correspondiesen a las frecuencias de clase mas altas. Además, si indicamos la posición del 1er, 2ndo y 3er cuartíl en cada barra sería de mucha utilidad para visualizar las medidas de posición y así hacerlas conmensurables con los desplazamientos.  Preparé un pequeño script en R para elaborar esas gráficas, que pueden ver a continuación:

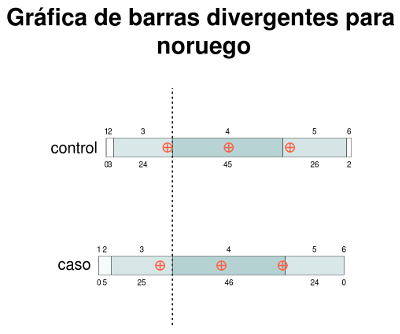
Las gráficas de arriba permiten una mejor comparación del rendimiento académico de los estudiantes de bajos ingresos familiares y aquel de la población estudiantíl en general.  Para el caso de la asignatura de "Noruego" (lengua primaria), no se observan diferencias importantes entre las calificaciones de uno y otro grupo.  Para el caso de "Inglés" (lengua secundaria) se observa un leve desplazamiento hacia las calificaciones más bajas de parte del grupo de estudiantes de bajos ingresos familiares (identificado como "caso").  Para matemáticas, se observa un desplazamiento más acentuado, en donde los estudiantes de bajos ingresos obtuvieron calificaciones más bajas.  Obsérvese que la barra horizontal de este grupo está más desplazada hacia la izquierda.

Coloco el código R abajo en este post para quien esté interesado.  Quizás incorpore este tipo de gráficas en mi librería estUNA, pero todavía lo considero en etapa experimental.

#la data es tomada del estudio en "3827_1.pdf"
matematicas <- data.frame (caso    = c(0.01,0.16,0.30,0.31,0.19,0.03),
                           control = c(0.01,0.05,0.26,0.43,0.22,0.03) )
ingles <- data.frame(caso    = c(0.01,0.08,0.25,0.40,0.24,0.02),
                     control = c(0.00,0.05,0.21,0.43,0.27,0.04) )
noruego <- data.frame(caso    = c(0.00,0.05,0.25,0.46,0.24,0.00),
                      control = c(0.00,0.03,0.24,0.45,0.26,0.02) )

graficar_barras_divergentes <- function(mdata,nombre=deparse(substitute(mdata))) {
  #esta función supone que mdata es un marco de datos
  #en donde cada columna se asocia a los porcentajes de los niveles
  #de una escala ordinal en orden ascendente (ie. el primer elemento del
  #vector se corresponde a la frecuencia del menor nivel en la escala).
  mdata_ac <- rbind(mdata,rep(0,ncol(mdata)))
  filas_par <- (nrow(mdata) %% 2 == 0)

  for (i in 1:ncol(mdata)) {
    x <- cumsum(mdata[[i]])
    if (filas_par)
      mid <- x[nrow(mdata) %/% 2]
    else
      mid <- x[nrow(mdata) %/% 2] + mdata[[i]][(nrow(mdata) %/% 2) + 1]/2
    mdata_ac[[i]] <- c(-mid,x -mid)
  }
  #crea un nuevo cuadro del tamaño adecuado
  frame()
  plot.window(xlim=c(min(mdata_ac)-0.2,max(mdata_ac)),ylim=c(0,0.5*ncol(mdata_ac)))
  #dibuja una línea vertical punteada de "centralidad"
  lines(c(0,0),c(0,0.5*ncol(mdata_ac)),lty="dotted")
  for (i in 1:ncol(mdata_ac) ) {
    #calcula la posición de las etiquetas para las frecuecias/categorias
    lbx <- (tail(mdata_ac[[i]],-1)+head(mdata_ac[[i]],-1))/2
    #dibuja los rectángulos que componen las frecuencias de cada clase
    for (j in 1:(nrow(mdata_ac)-1) )
      rect(mdata_ac[j,i], 0.21 + (i-1)*0.5 ,mdata_ac[j+1,i], 0.29 + (i-1)*0.5 ,
               col=rgb(95/256,158/256,160/256,alpha=mdata[j,i]) , lwd=0.25 )
    #escribe las frecuencias
      text(x=lbx,y=0.18+(i-1)*0.5,cex=0.4,labels=round(mdata[[i]]*100,digits=2) )
    #escribe las etiquetas de categorías
      text(x=lbx, y=0.32+(i-1)*0.5,cex=0.4,labels=rownames(mdata) )
    #indica los cuartiles
    #indica cuartiles
      points(seq(from=0.25,to=0.75,by=0.25)+mdata_ac[1,i],rep(0.25+(i-1)*0.5,3),col="tomato",pch=10)
  }
  #escribe las etiquetas de cada serie de datos
  text(x=min(mdata_ac)-0.1,y=seq(from=0.25,to=0.25+0.5*ncol(mdata),by=0.5),cex=0.8,labels=colnames(mdata) )
  #El titulo
  title(main=paste("Gráfica de barras divergentes para\n",nombre) )
}

ppi <- 300
png("gbd%2d.png",width=ppi*4,height=ppi*4,res=ppi)
graficar_barras_divergentes(matematicas)
graficar_barras_divergentes(ingles)
graficar_barras_divergentes(noruego)
graphics.off()
png("graficos_de_barras.png",width=ppi*4,height=ppi*6,res=ppi)
par(mfrow=c(3,2))
barplot(matematicas[[1]],names.arg=1:6,main="Matematicas",sub="(grupo caso)")
barplot(matematicas[[2]],names.arg=1:6,main="Matematicas",sub="(grupo control)")
barplot(ingles[[1]],names.arg=1:6,main="Ingles",sub="(grupo caso)")
barplot(ingles[[2]],names.arg=1:6,main="Ingles",sub="(grupo control)")
barplot(noruego[[1]],names.arg=1:6,main="Noruego",sub="(grupo caso)")
barplot(noruego[[2]],names.arg=1:6,main="Noruego",sub="(grupo control)")
graphics.off()

Bibliografía

• HASSAN, J. (2007). Parents’ socioeconomic status and children’s academic performance. Norwegian Social Research. NOVA Notat 7/2009.
• HEIBERGER, R. y ROBBINS, N. (2011). Plotting Likert and Other Rating Scales Section on Survey Research Methods – JSM 2011.

Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.