Como seguramente ustedes saben, los trabajos prácticos de estadística pasaron a ser evaluaciones formativas desde hace algunos semestres. A partir de entonces, el objetivo 1 de Estadística General (745) se evalúa en la primera parcial y en la integral. Aunque ya no es necesario entregar un trabajo práctico cómo tal ni recibirá una calificación departe mía, yo les recomendaría realizar las actividades contempladas en el enunciado del trabajo, que fueron publicadas aqui. La razón de mi recomendación es porque en este semestre, las actividades del trabajo práctico contemplan la elaboración de diagramas de caja y de torta. Mi olfato docente me obliga a avisarles sobre esto e invitarlos a que continúen leyendo esta entrada, donde realizaremos juntos las actividades propuestas, no vaya a ser que las gráficas de tortas y de caja los agarren desprevenidos este semestre...
Mostrando entradas con la etiqueta estadística descriptiva. Mostrar todas las entradas
Mostrando entradas con la etiqueta estadística descriptiva. Mostrar todas las entradas
lunes, 25 de julio de 2016
martes, 13 de mayo de 2014
Técnicas de visualización de datos a ser utilizadas este semestre
En este lapso académico se les pide a los estudiantes de Estadística General (745) realizar diagramas de tallo y hoja, ojivas de frecuencia y diagramas de caja como parte de las actividades prácticas del objetivo 1. En esta entrada, hablaré un poco sobre estas técnicas de visualización de datos y como se implementan en R / estUNA.
martes, 19 de noviembre de 2013
Estudio de estadística descriptiva en R /estUNA - video Tutorial
Video-tutorial sobre cómo utilizar el lenguaje R y la librería estUNA para realizar análisis exploratorio de datos como los que se piden en los trabajos prácticos de Estadística General (745):
Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.
miércoles, 27 de marzo de 2013
The Lending Club - Parte II
Para comenzar a trabajar con este ejemplo
En la primera parte de esta serie de entradas, se expuso la información de contexto sobre el problema del Lending Club. En la siguiente parte, se hará el ejercicio de construcción de modelos de regresión lineal.
La data con la que se trabajará para este ejemplo está disponible para su descarga desde este enlace. Una vez descargado ese archivo, colóquelo en su directorio de trabajo de R, que usualmente será "Mis Documentos" en el caso de Windows. Para trabajar con este ejemplo, también debe tener la librería "estUNA" en su directorio de trabajo (consulte esta en si tiene dudas sobre cómo descargar estUNA y colocarla en su directorio de trabajo).
Sobre la data del problema del "Lending Club"
El archivo identificado arriba "lending_club.Rda" contiene un data frame identificado como loandata. A continuación se detallan las variables contenidas en loandata como columnas.
| Identificador de variable | Descripción |
| Ar | (Amount Requested) Monto solicitador por el prestatario para financiamiento. |
| Af | (Amount Funded) Monto financiado. |
| Ir | (Interest Rate) Tasa de Interés del financiamiento. Esta es la variable dependiente. |
| Ld | (Loan Duration) Variable categórica correspondiente a la duración del préstamo (36 o 60 meses). |
| Lp | (Loan Purpose) Variable categórica correspondiente al propósito del préstamo. |
| DtIR | (Debt-to-income Ratio) Coeficiente de deuda sobre ingresos. |
| St | (State) Código de dos letras correspondiente al estado de residencia del prestatario. |
| Ho | (Home ownership) Tipo de propiedad sobre la casa: "NONE" es ninguna casa, "MORTGAGE" indica hipoteca sobre la casa, "OWN" indica que la casa es propia y "RENT" indica que la casa es alquilada. |
| I | (Income) Ingreso mensual. |
| Fi | (FICO) Puntuación FICO del solicitante. |
| Ocl | (Open Credit Lines) Cantidad de líneas de crédito abiertas del solicitante. |
| Rcb | (Rotating credit balance) Balance rotativo de credito. |
| Inq | (Inquiries) Número de veces que algún comercio ha solicitado un reporte crediticio certificado. |
| Ed | (Employment duration) Tiempo en el actual empleo. |
En todo informe de análisis de datos, es importante indicar el tamaño de la muestra empleada en el estudio. El data frame loandata consta de 2492 observaciones (o renglones) y 14 variables (o columnas).
Análisis exploratorio de los datos
Antes de emprender el planteamiento de los modelos de regresión para inferir cuales variables, en definitiva, inciden sobre la fijación de la tasa de interés de un préstamo, es conveniente realizar un análisis exploratorio de los datos. En un análisis exploratorio se utilizan técnicas de la estadística descriptiva para "descubrir" el comportamiento de las variables, su variabilidad inherente y la variabilidad conjunta entre las mismas.El análisis exploratorio nos debe conducir a plantear uno o varios modelos de regresión viables y a entender cómo o donde estos pueden fallar.
A continuación damos el script en R que realiza los distintos pasos del análisis exploratorio. Si va a experimentar con este script en su computadora, recuerde que debe tener el archivo de la librería estUNA y el archivo de data lending_club.Rda en su directorio de trabajo. Seguidamente iremos interpretando los resultados.
A continuación damos el script en R que realiza los distintos pasos del análisis exploratorio. Si va a experimentar con este script en su computadora, recuerde que debe tener el archivo de la librería estUNA y el archivo de data lending_club.Rda en su directorio de trabajo. Seguidamente iremos interpretando los resultados.
load("estUNA")Como primer paso del análisis exploratorio, se genera un resumen con las principales estadísticas del data frame. Esto lo hace la instrucción summary(loandata), tras lo cual se imprime lo siguiente:
load("lending_club.Rda")
attach(loandata)
options(width=60)
png("exploratorio%02d.png")
#Imprime un resúmen del data frame
summary(loandata)
#Matriz de correlación entre las variables cuantitativas
cor(loandata[,c("Ar","Af","Fi","I","Ocl","Rcb","Inq","Ir")])
#La primera gráfica es un histograma de Ir
graficar(Ir)
#A continuación unas graficas de dispersión
#Grafica la tasa de intereses (eje Y) versus:
graficar.dispersion(Ar,Ir,cex=0.2,pch=19)
#Monto solicitado
graficar.dispersion(Af,Ir,cex=0.2,pch=19)
#Monto financiado
graficar.dispersion(Fi,Ir,cex=0.2,pch=19)
#Puntuación FICO
graficar.dispersion(I,Ir,cex=0.2,pch=19)
#Ingreso mensual
graficar.dispersion(Ocl,Ir,cex=0.2,pch=19)
#Lin. credito abiertas
graficar.dispersion(DtIR,Ir,cex=0.2,pch=19)
#Deuda/Ingresos
graficar.dispersion(Rcb,Ir,cex=0.2,pch=19)
#Balance crédito rotativo
graficar.dispersion(Inq,Ir,cex=0.2,pch=19)
#Cantidad de indagaciones
#Diagramas de caja comparativos
#Grafica la relación entre la tasa de interés
#y las siguientes variables categóricas:
caja(Ir,Ho) #Propiedad de la vivienda
caja(Ir,Ed) #Tiempo en el empleo actual
caja(Ir,Ld) #Plazo de financiamiento (36 o 60 meses)
#Para las siguientes dos variables, la visualización
#más adecuada es una tabla.
#Estudia la variabilidad de las tasas de interés según:
#1) El propósito del prestamo (Lp)
lp_mat <- t(sapply(levels(Lp),
function(s)
c(sum(Lp==s), median(Ir[Lp==s]),
wilcox.test(Ir~Lp==s)\(\$\)p.value)
)
)
colnames(lp_mat) <- c("frec","mediana","p_valor")
lp_mat <- as.data.frame(lp_mat)
lp_mat <- lp_mat[order(lp_mat\(\$\)frec,decreasing=TRUE),]
lp_mat
#2) El estado de residencia del prestatario:
st_mat <- t(sapply(levels(St),
function(s)
c(sum(St==s), median(Ir[St==s]),
wilcox.test(Ir~St==s)\(\$\)p.value)
)
)
colnames(st_mat) <- c("frec","mediana","p_valor")
st_mat <- as.data.frame(st_mat)
st_mat <- st_mat[order(st_mat\(\$\)frec,decreasing=TRUE),]
st_mat
Ar Af Ir Ld
Min. : 1000 Min. : 200 Min. :0.0542 36:1944
1st Qu.: 6000 1st Qu.: 6000 1st Qu.:0.1016 60: 548
Median :10000 Median :10000 Median :0.1311
Mean :12431 Mean :12038 Mean :0.1308
3rd Qu.:17000 3rd Qu.:16000 3rd Qu.:0.1580
Max. :35000 Max. :35000 Max. :0.2489
Lp DtIR St
debt_consolidation:1306 Min. :0.0000 CA : 432
credit_card : 442 1st Qu.:0.0975 NY : 253
other : 197 Median :0.1533 TX : 174
home_improvement : 152 Mean :0.1540 FL : 169
major_purchase : 101 3rd Qu.:0.2068 IL : 101
small_business : 87 Max. :0.3491 GA : 97
(Other) : 207 (Other):1266
Ho I Fi
MORTGAGE:1146 Min. : 588.5 Min. :642.5
NONE : 0 1st Qu.: 3500.0 1st Qu.:682.5
OTHER : 5 Median : 5000.0 Median :702.5
OWN : 200 Mean : 5687.6 Mean :708.4
RENT :1141 3rd Qu.: 6800.0 3rd Qu.:727.5
Max. :102750.0 Max. :832.5
Ocl Rcb Inq
Min. : 2.00 Min. : 0 Min. :0.0000
1st Qu.: 7.00 1st Qu.: 5612 1st Qu.:0.0000
Median : 9.00 Median : 10978 Median :0.0000
Mean :10.07 Mean : 15263 Mean :0.9013
3rd Qu.:13.00 3rd Qu.: 18900 3rd Qu.:1.0000
Max. :38.00 Max. :270800 Max. :9.0000
Ed
10+ :653
< 1 :247
2 :244
3 :234
5 :201
4 :192
(Other):721
Para las variables cuantitativas, la instrucción summary(...) devuelve una tabla con las principales medidas de posición (mínimo, 1er cuartíl, mediana y media, 3er cuartíl, máximo). Para las variables categóricas (o variables tipo "factor", como se les conoce en R), summary(...) devuelve una tabla de frecuencias para algunos niveles de la variable (los más frecuentes). Estos resultados permiten apreciar rápidamente cuál rango de valores asume cada variable. Por ejemplo, podemos observar que la distribución de la variable Ar, en términos de los estadísticos de posición más importantes, es bastante similar a la de la variable Af. Esto tiene bastante sentido, pues esperaríamos que el monto solicitado y el monto financiado sean muy parecidos, una vez aprobado el préstamo. Nótese el uso de la instrucción attach(...) al principio del script para referirse fácilmente a las variables de loandata en lo sucesivo.
Otra tabla bastante útil en un análisis exploratorio es la tabla de las correlaciones entre las variables. Esto por cierto sería muy útil para estudiar la colinealidad o multicolinealidad de las variables, según se exige para el trabajo de este semestre. La instrucción cor(...) en R genera una matriz cuadrada de correlaciones entre todas las variables. Como cada variable está perfectamente correlacionada consigo misma, los elementos de la diagonal son todos "1". De hecho, una correlación de "1" o "-1" indica una colinealidad perfecta entre dos variables. Puede consultar más sobre esto en el artículo de wikipedia sobre correlación lineal. La matriz de correlación sólo tiene sentido para variables cuantitativas del data frame, lo cual en este caso se determina por medio de la instrucción cor(loandata[,c("Ar","Af","Fi","I","Ocl","Rcb","Inq","Ir")]) :
Ar Af Fi I
Ar 1.00000000 0.97022602 0.083040383 0.39109060
Af 0.97022602 1.00000000 0.073791988 0.37468574
Fi 0.08304038 0.07379199 1.000000000 0.12355539
I 0.39109060 0.37468574 0.123555388 1.00000000
Ocl 0.19680145 0.18779714 -0.090039520 0.17180076
Rcb 0.29277055 0.26116166 0.003217914 0.35936379
Inq -0.02721561 -0.06224654 -0.092828774 0.03398569
Ir 0.33141077 0.33627376 -0.709911785 0.01231114
DtIR 0.07985656 0.09177385 -0.217596139 -0.16376264
Ocl Rcb Inq Ir
Ar 0.19680145 0.292770550 -0.02721561 0.33141077
Af 0.18779714 0.261161657 -0.06224654 0.33627376
Fi -0.09003952 0.003217914 -0.09282877 -0.70991178
I 0.17180076 0.359363787 0.03398569 0.01231114
Ocl 1.00000000 0.290582979 0.10790657 0.09109025
Rcb 0.29058298 1.000000000 0.01285580 0.06042262
Inq 0.10790657 0.012855801 1.00000000 0.16846322
Ir 0.09109025 0.060422621 0.16846322 1.00000000
DtIR 0.37172725 0.188286897 0.01126195 0.17143913
DtIR
Ar 0.07985656
Af 0.09177385
Fi -0.21759614
I -0.16376264
Ocl 0.37172725
Rcb 0.18828690
Inq 0.01126195
Ir 0.17143913
DtIR 1.00000000
Por razones tipográficas de espacio, la matriz de correlación de arriba se dividió en tres segmentos: el primero con las primeras cuatro columnas de la matriz, el segundo en el renglón de abajo con las siguientes cuatro columnas de la matriz y la última columna de la matriz en el tercer renglón. Nótese que la correlación de cada variable consigo misma es "1". También se puede observar que las variables Ar y Af están muy correlacionadas (correlación mayor a 97%). Esto implica que incluir ambas variables en un mismo modelo de regresión lineal puede generar un problema de colinealidad o multicolinealidad (para más detalles, puede consultar la sección 14.4 del libro "Probabilidad y Estadística" de G. Canavos). Ya se había comentado anteriormente sobre la relación (semántica) entre ambas variables- en lo sucesivo consideraremos solamente a la variable Ar, porque el monto solicitado del financiamiento es la información previa necesaria para decidir el monto a financiar y la tasa de interés del crédito. También podemos notar que la puntuación FICO (Fi) y la tasa de interés (Ir) tienen bastante correlación (-0.71). Esto indica que la variable Fi es una buena candidata para incluirse en un modelo de regresión lineal con la tasa de interés como variable dependiente. Además, el signo negativo de la correlación indica que el coeficiente de regresión para la variable Fi en el modelo lineal también debería ser negativo.
La puntuación FICO del solicitante está muy correlacionada con la tasa de interés del préstamo. Pero a su vez, como vimos en la primera parte de esta serie (The Lending Club - Parte I), muchas de las variables en este data frame son tomadas en cuenta para el cálculo de la calificación FICO. Entonces, por una parte esperaríamos cierta correlación entre esas variables y la calificación FICO. Si esas variables se incluyen en el modelo lineal, pudiésemos estar ante un problema de variables de confusión (confounder variables). Las variables de confusión son aquellas que están correlacionadas con la variable dependiente y con alguna o algunas de las otras variables independientes del modelo. El problema que generan las variables de confusión es que a veces, sus efectos sobre la variable dependiente pueden ser exagerados. También puede ocurrir lo que se llama un efecto supresor. Puede consultar más sobre estos temas en este blog. Por nuestra parte, algunos de estos conceptos saldrán a relucir a medida que iremos ensayando distintos modelos de regresión lineal.
A continuación podemos observar algunas gráficas. La primera (Fig. 1) es un histograma de las tasas de interés:
 Esta variable tiene una distribución casi acampanada ... ¡Un momento! ¿Qué es ese segundo pico que se observa a la izquierda, en el intervalo [0,06 - 0,08)? Bueno, una variable así difícilmente sea normalmente distribuida, lo cual no es un problema en sí. Sin embargo, llama la atención que exista un grupo tan significativo de prestamos con tasas de interés en ese rango. Quizás, alguna de las variables independientes pueda explicar ese comportamiento...
Esta variable tiene una distribución casi acampanada ... ¡Un momento! ¿Qué es ese segundo pico que se observa a la izquierda, en el intervalo [0,06 - 0,08)? Bueno, una variable así difícilmente sea normalmente distribuida, lo cual no es un problema en sí. Sin embargo, llama la atención que exista un grupo tan significativo de prestamos con tasas de interés en ese rango. Quizás, alguna de las variables independientes pueda explicar ese comportamiento...
Seguimos con la parte más ilustrativa de nuestro análisis exploratorio, que son las gráficas de dispersión entre la tasa de interés y las otras variables cuantitativas (Fig. 2):
La puntuación FICO del solicitante está muy correlacionada con la tasa de interés del préstamo. Pero a su vez, como vimos en la primera parte de esta serie (The Lending Club - Parte I), muchas de las variables en este data frame son tomadas en cuenta para el cálculo de la calificación FICO. Entonces, por una parte esperaríamos cierta correlación entre esas variables y la calificación FICO. Si esas variables se incluyen en el modelo lineal, pudiésemos estar ante un problema de variables de confusión (confounder variables). Las variables de confusión son aquellas que están correlacionadas con la variable dependiente y con alguna o algunas de las otras variables independientes del modelo. El problema que generan las variables de confusión es que a veces, sus efectos sobre la variable dependiente pueden ser exagerados. También puede ocurrir lo que se llama un efecto supresor. Puede consultar más sobre estos temas en este blog. Por nuestra parte, algunos de estos conceptos saldrán a relucir a medida que iremos ensayando distintos modelos de regresión lineal.
A continuación podemos observar algunas gráficas. La primera (Fig. 1) es un histograma de las tasas de interés:
Fig. 1 - Histograma de las tasas de interés

Seguimos con la parte más ilustrativa de nuestro análisis exploratorio, que son las gráficas de dispersión entre la tasa de interés y las otras variables cuantitativas (Fig. 2):
Fig. 2 - Gráficas de dispersión de las variables independientes cuantitativas respecto a la variable dependiente Ir.
 (a) Ar / Ir
|

(b) Fi / Ir
|
 |
 |
 |
 |
 |
Los diagramas de dispersión de la Figura 2 confirman que, entre todas las variables independientes, la calificación FICO (Fi) es la más fuertemente asociada a la tasa de interés (Ir). Esto era de esperarse, pero el diagrama de dispersión de la Figura 2.b. revela más detalles sobre esta asociación: la curva lowess (la línea verde oscura) tiene la misma pendiente hasta una puntuación FICO de 750 (aproximadamente, o a pepa de ojo). A partir de 750 puntos en la calificación FICO, la pendiente de la curva lowess se hace más horizontal. Esto implica que a mayor puntuación FICO, menor tasa de interés del préstamo, pero a partir de 750 puntos FICO, la diferencia no es tan grande. Dado la magnitud de la asociación entre estas dos variables, la recta lineal quizás no sea el tipo de asociación más idónea entre estas variables.
Otro patron marcado según la curva lowess se puede observar (ver Figura 2.a) en la asociación del monto solicitado para el financiamiento (Ar) y la tasa de interés (Ir), aunque esta asociación no es tan marcada como la asociación Fi-Ir, cuyos puntos en el diagrama de dispersión son menos dispersos respecto a la curva lowess. También se observa una relación creciente entre la cantidad de líneas de crédito abiertas y la tasa de interés (Figura 2.d). Esta asociación podría no ser no-lineal, dado la convexidad de la curva lowess que se observa en la gráfica.
La variable DtIr (relación Deuda-Ingresos) también tiene una asociación creciente con la tasa de interés (ver Figura 2.e). Sin embargo, dada la baja correlación entre estas variables (de apenas 0.17 según la matriz de correlación de arriba) y el alto grado de dispersión de los puntos, es posible que esta variable no sea significativa en un modelo de regresión. La Figura 2.g revela un patrón interesante: para 0 indagaciones (solicitudes de reportes de historial crediticio), las tasas de interés son más bajas. Para 1 o más indagaciones, las tasas de interés no difieren significativamente. Esto indica que posiblemente sea conveniente transformar la variable Inq a una variable indicadora según sea Inq=0 o no.
Las otras dos variables, ingresos mensuales (I) y balance rotativo de crédito (Rcb) contienen muchos datos atípicos hacia el extremo derecho para ser útiles. Estos datos atípicos (en forma de ingresos mensuales astronomicamente altos por ejemplo) podrían afectar la regresión en formas no deseadas, por lo cual su inclusión en un modelo de regresión quizás no sea una buena idea.
Para explorar la asociación entre la tasa de interés y otras variables categóricas, lo más conveniente es usar diagramas de caja comparativos. Así se hizo para las variables Ho, Ed y Ld, como se muestra en la Figura 3:
|
(a) Ir ~ Ho
|
(b) Ir ~ Ed
|
(c) Ir ~ Ld
|
Las primeras dos gráficas de caja (Figuras 3.a y 3.b) no revelan asociaciones significativas entre la tasa de interés y las respectivas variables. En contraste, La Figura 3.c indica que si hay una relación significativa entre la tasa de interés y la duración del préstamo: los prestamos de 36 meses tienen tasas de interés signficativamente más bajas.
Para las otras dos variables cualitativas - el estado de residencia (St) y el propósito del préstamo (Lp) - no se hicieron diagramas de caja comparativos porque estas variables tienen demasiados niveles (46 estados y 14 propósitos de préstamo diferentes). Para cada una de estas variables, se optó por generar tablas indicando la frecuencia de cada nivel, la tasa de interés mediana y el p-valor del contraste Wilcoxon de diferencia entre medianas (consultar el artículo en Wikipedia). La idea es verificar si para algún nivel determinado de estas variables, las tasas de interés difieren significativamente de aquellas asociadas a los otros niveles. Para la variable estado (St):
frec mediana p_valor
CA 432 0.13110 0.69246237
NY 253 0.13110 0.82515314
TX 174 0.13110 0.30747046
FL 169 0.13110 0.88525055
IL 101 0.12530 0.22145716
GA 97 0.12180 0.27619025
PA 96 0.13045 0.23581778
NJ 92 0.12120 0.38675613
VA 78 0.12550 0.78497883
MA 73 0.12120 0.38183801
OH 71 0.12230 0.10542538
MD 68 0.13790 0.62463807
NC 64 0.12405 0.34075690
CO 61 0.13110 0.92712927
WA 58 0.13110 0.89902872
CT 50 0.13140 0.29789052
AZ 46 0.13110 0.86390489
MI 45 0.14090 0.01538049
MN 38 0.13545 0.34930242
: : : :
: : : :
Esta tabla (dada aquí de forma parcial) enumera los 46 estados en orden descendente por frecuencia de observaciones. Podemos observar que para el estado MI (Michigan), la tasa de interés mediana es significativamente distinta de la de los otros estados (con un p-valor de 1% en el contraste de Wilcoxon). Esto implica que los prestamos de los solicitantes de ese estado tienen una tasa de interés más alta, por alguna razón. Sin embargo, como solo 45 de las 2492 observaciones son de ese estado, incluir la variable St en un modelo de regresión lineal solamente para ajustar mejor a un grupo que representa menos del 2% de las observaciones sería un despropósito. Seguidamente tenemos una tabla similar para el propósito del prestamo:
frec mediana p_valor
debt_consolidation 1306 0.13490 6.704956e-11
credit_card 442 0.13110 9.769974e-01
other 197 0.13060 6.911076e-01
home_improvement 152 0.11130 2.162582e-06
major_purchase 101 0.11120 2.559098e-08
small_business 87 0.12840 6.169896e-01
car 50 0.10475 9.231269e-04
wedding 39 0.12210 2.223396e-01
medical 30 0.13110 8.066417e-02
moving 29 0.13110 6.110691e-01
vacation 21 0.12120 3.160609e-01
house 20 0.13085 8.177116e-01
educational 14 0.09755 4.628680e-02
renewable_energy 4 0.09130 1.336665e-01
Para esta variable, si se observa un subgrupo grande (con 1306 observaciones), cuya tasa de interés difiere significativamente de la de otros grupos (p-valor casi nulo). Este grupo es el grupo de prestatarios que solicitaron un préstamo para consolidación de deudas (debt consolidation). Existen otros grupos con tasas de interés significativamente distintas, pero son muy pequeños en relación con el número total de observaciones. Por cierto, la tasa de interés mediana de los prestamos solicitados para consolidación de deudas (13,49%) es mayor a la tasa de interés mediana general (13,11%). De esto se deduce que sería conveniente incluir una variable indicadora en el modelo de regresión según sea el propósito del préstamo la consolidación de deudas o no.
Análisis exploratorio de datos - algunas conclusiones
Tras realizar el ejercicio anterior, podemos concluir sobre la importancia de explorar los datos antes de construir los modelos de regresión. Las observaciones realizadas tras este estudio exploratorio se pueden aunar al conocimiento o a las ideas previas que tenemos sobre la temática que estamos estudiando (en este caso, los prestamos personales en EEUU). Esto ayudará a plantear posibles hipótesis sobre las relaciones de las variables en forma de modelos de regresión lineal. Es importante destacar que un análisis exploratorio no es inferencial. Todo lo que observamos hasta este punto queda en forma de conjetura y no es generalizable a la población. Cuando, tras realizar el ajuste por mínimos cuadrados de un modelo de regresión lineal, tenemos los p-valores de la prueba F, los estadísticos T-Student de significatividad de los coeficientes poblacionales y cuando finalmente realicemos un análisis de residuos para validar el modelo, si tendremos los elementos estadísticos requeridos para un estudio inferencial. El análisis exploratorio sirve para guiar al análisis de regresión, el cual haremos en la tercera y última parte de estas entradas del blog...
Como citar esta entrada
Romero, J. (Marzo, 2013). The Lending Club - parte II. [Entrada de blog]. Recuperado desde https://unamatematicaseltigre.blogspot.com/2013/03/the-lending-club-parte-ii.html.
Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.
Etiquetas:
738,
745,
746,
748,
análisis exploratorio de datos,
es,
estadística descriptiva,
estUNA,
multicolinealidad,
R,
regresión lineal,
visualización de datos
miércoles, 23 de enero de 2013
Consideraciones sobre la visualización de datos - parte 2
Continuamos con la serie de entradas sobre la visualización de datos, esta vez complementando un poco lo dicho sobre las gráficas de torta en la entrada pasada. ¿Cuándo deben o no usarse? ¿Cómo se deben usar?
En el semestre pasado 2012-1, la data del trabajo práctico versaba sobre un estudio de nutrición infantil donde se estudiaban varios factores conjuntamente como el Índice de Masa corporal, el peso, la estatura y la actividad física, entre otros. Para la asignatura de Estadística General (745), se requería, entre otras cosas, elaborar una gráfica de torta para la variable X7 - el índice de actividad física. A continuación muestro una típica gráfica de estas. Nótese que en el ejemplo de abajo, la gráfica de tortas es tridimensional, por lo cuál le hice observaciones al estudiante según las explicaciones en la entrada anterior. Para el trabajo final, los estudiantes re-elaboraron estas gráficas de torta en dos dimensiones, con lo cual dieron cumplimiento a la actividad correspondiente requerida en el enunciado del trabajo. Sin embargo - y con la presión del semestre ya dejada atrás, le invito a echar un segundo vistazo a esta gráfica. Aparte de la tridimensionalidad, ¿nota algún otro problema con esta gráfica?

Es necesario considerar el tipo de variable o la escala de X7. Si observa la leyenda a la derecha, verá que los niveles o valores del índice de actividad física son: sedentario, ligera, moderada, alta y muy alta. En efecto, la variable X7 se refiere a la intensidad o la frecuencia de actividad física de los individuos de la muestra. Podemos establecer comparaciones de orden entre estos niveles de actividad física. Por ejemplo, una persona con actividad moderada tiene menos actividad física que otra persona cuyo nivel de actividad es "alta". En resumen, X7 es una variable de escala ordinal. ¿Qué tiene esto que ver con las gráficas de torta?
En teoría, las gráficas de torta permiten visualizar el valor modal de una muestra. El valor modal es aquel con mayor frecuencia y por lo tanto el sector correspondiente en la gráfica de torta se verá más grande. Sin embargo, la variable X7 es una variable ordinal. Sus niveles tienen una jerarquía, un orden de menor a mayor. Gracias a ese orden jerárquico de sus niveles, la variable X7 tiene mediana, aparte de tener moda. Por cierto, la moda de esta variable es "actividad física alta" y su mediana es "actividad física moderada".
La gráfica de torta de arriba es deficiente. No logra comunicar toda la estructura jerárquica de orden que la variable X7 posee por ser una variable ordinal. En efecto, en una circunferencia no hay ningún punto privilegiado, no hay un cero natural, pues dejaría de serlo al rotar la circunferencia. Si uno recorre la circunferencia en cualquier dirección, regresa al punto de partida y por lo tanto en una circunferencia tampoco hay una dirección que esté asociada con "más de algo" o "menos de algo". Es decir, en una circunferencia no podemos reflejar ninguna jerarquía de orden. Si la gráfica de torta no es el tipo de gráfica más adecuada para resumir visualmente esta variable, ¿cuáles otros tipos de gráfica deberíamos de considerar?

La gráfica de barras es una alternativa natural para visualizar variables de escala ordinal cómo la variable X7. Si en el eje de las abscisas disponemos los niveles de X7 de menor a mayor (en la gráfica de arriba los niveles de actividad tienen una codificación numérica de 1.0 a 1.8) y hacemos corresponder los valores de las frecuencias en el eje de las ordenadas, las alturas de las barras encima de cada nivel de las abscisas nos permite visualizar la forma de la distribución de la variable X7. Aparte de poder visualizar la moda tal como en la gráfica de tortas, una gráfica de barras permite visualizar la asimetría, la dispersión y la forma general de la distribución de frecuencias, lo cual no podíamos hacer con una gráfica de tortas. Ampliando un poco más esta gráfica, podríamos por ejemplo señalar la clase mediana.
Sin embargo, sobre este último punto surge una inquietud respecto a si no existirá otro tipo de gráfica más "informativa" para variables de escala ordinal. Un tipo de gráfica que permita señalar la diferencia entre la moda (o las modas) y la mediana y - ¿porqué no? - también se señalen los cuartiles para visualizar mejor el grado de dispersión. Sería interesante también que con esta gráfica se pudiesen comparar fácilmente diferentes poblaciones o grupos de una variable ordinal, para verificar cambios en la tendencia central de un grupo a otro. Si bien existen las gráficas de cajas comparativas, en las cuales las hendiduras indican posibles diferencias significativas entre las medianas de unos u otros subgrupos, la gráfica de caja (o boxplot) no es a mi criterio la más adecuada cuando las variables ordinales tienen pocos niveles (o categorías ordinales). Además, con las gráficas de cajas no podemos visualizar la moda o la distribución de frecuencias de la variable en las categorías ordinales.
Para poner las cosas en perspectiva, en la discusión que sigue voy a considerar un estudio sobre el rendimiento académico de jóvenes noruegos entre 13 y 15 años de edad y el nivel de ingresos familiar [Ver Hassan(2007)]. En este estudio, se consideraron dos grupos: uno llamado "grupo control", representado por una muestra de estudiantes sin distinción del nivel de ingresos familiar y otro grupo - el "grupo caso" - representado por una muestra de estudiantes provenientes de hogares con un ingreso agregado ubicado en el 60% o menos del ingreso familiar mediano en Noruega. Se consideraron las notas de estos estudiantes para tres áreas claves: Matemáticas, Inglés y Noruego. Como en Noruega las notas son de la escala entre 1 y 6, siendo el "6" la nota más alta, la variable asociada al rendimiento académico en cada área es en efecto una variable ordinal. Las distribuciones de las notas (en porcentajes) correspondientes a los subgrupos "caso" y "control" para las tres áreas de conocimiento respectivas son dadas según la siguiente tabla:
| Matemática | Inglés | Noruego | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Caso | Control | Caso | Control | Caso | Control | ||||||
| Nota | Frec | Nota | Frec | Nota | Frec | Nota | Frec | Nota | Frec | Nota | Frec |
| 1 | 1% | 1 | 1% | 1 | 1% | 1 | 0% | 1 | 0% | 1 | 0% |
| 2 | 16% | 2 | 5% | 2 | 8% | 2 | 5% | 2 | 5% | 2 | 3% |
| 3 | 30% | 3 | 26% | 3 | 25% | 3 | 21% | 3 | 25% | 3 | 24% |
| 4 | 31% | 4 | 43% | 4 | 40% | 4 | 43% | 4 | 46% | 4 | 45% |
| 5 | 19% | 5 | 22% | 5 | 24% | 5 | 27% | 5 | 24% | 5 | 26% |
| 6 | 3% | 6 | 3% | 6 | 2% | 6 | 4% | 6 | 0% | 6 | 2% |
¿Cómo podríamos comparar los subgrupos de "caso" y "control" a través de las tres áreas de conocimiento mediante una gráfica? Si hiciéramos múltiples gráficas de barras, se vería como en la gráfica a la derecha.
¿Sirve éste resumen gráfico a los fines comparativos de detectar diferencias entre el rendimiento académico de estudiantes de bajos ingresos familiares y la población estudiantil en general?
Para las tres áreas académicas, la calificación modal de un grupo y otro es "4", por lo cual no se pueden detectar diferencias entre uno y otro subgrupo si solamente se toma en cuenta la moda. Más sin embargo, en el caso de la asignatura de matemáticas, se observa cierto desplazamiento hacia las calificaciones más bajas para el subgrupo de estudiantes con menores ingresos familiares. |
 |
Cómo los diagramas de barras de arriba no incluyen otros indicadores de tendencia central o de posición, es difícil establecer comparaciones más precisas. Además, un buen resumen gráfico de esta data debería de permitir constatar "desplazamientos" entre las calificaciones de un grupo y de otro.
Con esta idea de visualizar los "desplazamientos de las calificaciones" me puse a buscar sobre técnicas gráficas alternativas y di con un artículo en el cual el autor elaboraba sobre un tipo de gráficas llamada "gráficas de barras apiladas divergentes". En este tipo de gráficas, se empatan barras horizontales cuya longitud es proporcional a la frecuencias de los niveles consecutivos de la variable ordinal para cada subgrupo poblacional, formando una sola barra horizontal para cada subgrupo respectivo con varias barras apiladas de izquierda a derecha. Estas barras horizontales compuestas de varias barras apiladas se desplazan de modo que el punto cero se ubique en el medio de la clase central de la escala ordinal (para el caso en que el número de clases de la escala sea un número impar) o entre las dos clases del medio si el número de clases es par. De este modo, cuando colocamos las barras horizontales de cada subgrupo una encima de la otra de tal manera que todos los puntos "cero" estén alineados en una recta vertical, podemos constatar visualmente los desplazamientos entre uno y otro subgrupo.
Adicionalmente, pensé que sería buena idea sombrear las barras apiladas de cada barra horizontal de modo que los tonos más oscuros se correspondiesen a las frecuencias de clase mas altas. Además, si indicamos la posición del 1er, 2ndo y 3er cuartíl en cada barra sería de mucha utilidad para visualizar las medidas de posición y así hacerlas conmensurables con los desplazamientos. Preparé un pequeño script en R para elaborar esas gráficas, que pueden ver a continuación:
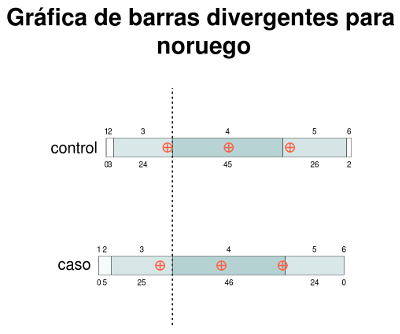


Las gráficas de arriba permiten una mejor comparación del rendimiento académico de los estudiantes de bajos ingresos familiares y aquel de la población estudiantíl en general. Para el caso de la asignatura de "Noruego" (lengua primaria), no se observan diferencias importantes entre las calificaciones de uno y otro grupo. Para el caso de "Inglés" (lengua secundaria) se observa un leve desplazamiento hacia las calificaciones más bajas de parte del grupo de estudiantes de bajos ingresos familiares (identificado como "caso"). Para matemáticas, se observa un desplazamiento más acentuado, en donde los estudiantes de bajos ingresos obtuvieron calificaciones más bajas. Obsérvese que la barra horizontal de este grupo está más desplazada hacia la izquierda.
Coloco el código R abajo en este post para quien esté interesado. Quizás incorpore este tipo de gráficas en mi librería estUNA, pero todavía lo considero en etapa experimental.
#la data es tomada del estudio en "3827_1.pdf"
matematicas <- data.frame (caso = c(0.01,0.16,0.30,0.31,0.19,0.03),
control = c(0.01,0.05,0.26,0.43,0.22,0.03) )
ingles <- data.frame(caso = c(0.01,0.08,0.25,0.40,0.24,0.02),
control = c(0.00,0.05,0.21,0.43,0.27,0.04) )
noruego <- data.frame(caso = c(0.00,0.05,0.25,0.46,0.24,0.00),
control = c(0.00,0.03,0.24,0.45,0.26,0.02) )
graficar_barras_divergentes <- function(mdata,nombre=deparse(substitute(mdata))) {
#esta función supone que mdata es un marco de datos
#en donde cada columna se asocia a los porcentajes de los niveles
#de una escala ordinal en orden ascendente (ie. el primer elemento del
#vector se corresponde a la frecuencia del menor nivel en la escala).
mdata_ac <- rbind(mdata,rep(0,ncol(mdata)))
filas_par <- (nrow(mdata) %% 2 == 0)
for (i in 1:ncol(mdata)) {
x <- cumsum(mdata[[i]])
if (filas_par)
mid <- x[nrow(mdata) %/% 2]
else
mid <- x[nrow(mdata) %/% 2] + mdata[[i]][(nrow(mdata) %/% 2) + 1]/2
mdata_ac[[i]] <- c(-mid,x -mid)
}
#crea un nuevo cuadro del tamaño adecuado
frame()
plot.window(xlim=c(min(mdata_ac)-0.2,max(mdata_ac)),ylim=c(0,0.5*ncol(mdata_ac)))
#dibuja una línea vertical punteada de "centralidad"
lines(c(0,0),c(0,0.5*ncol(mdata_ac)),lty="dotted")
for (i in 1:ncol(mdata_ac) ) {
#calcula la posición de las etiquetas para las frecuecias/categorias
lbx <- (tail(mdata_ac[[i]],-1)+head(mdata_ac[[i]],-1))/2
#dibuja los rectángulos que componen las frecuencias de cada clase
for (j in 1:(nrow(mdata_ac)-1) )
rect(mdata_ac[j,i], 0.21 + (i-1)*0.5 ,mdata_ac[j+1,i], 0.29 + (i-1)*0.5 ,
col=rgb(95/256,158/256,160/256,alpha=mdata[j,i]) , lwd=0.25 )
#escribe las frecuencias
text(x=lbx,y=0.18+(i-1)*0.5,cex=0.4,labels=round(mdata[[i]]*100,digits=2) )
#escribe las etiquetas de categorías
text(x=lbx, y=0.32+(i-1)*0.5,cex=0.4,labels=rownames(mdata) )
#indica los cuartiles
#indica cuartiles
points(seq(from=0.25,to=0.75,by=0.25)+mdata_ac[1,i],rep(0.25+(i-1)*0.5,3),col="tomato",pch=10)
}
#escribe las etiquetas de cada serie de datos
text(x=min(mdata_ac)-0.1,y=seq(from=0.25,to=0.25+0.5*ncol(mdata),by=0.5),cex=0.8,labels=colnames(mdata) )
#El titulo
title(main=paste("Gráfica de barras divergentes para\n",nombre) )
}
ppi <- 300
png("gbd%2d.png",width=ppi*4,height=ppi*4,res=ppi)
graficar_barras_divergentes(matematicas)
graficar_barras_divergentes(ingles)
graficar_barras_divergentes(noruego)
graphics.off()
png("graficos_de_barras.png",width=ppi*4,height=ppi*6,res=ppi)
par(mfrow=c(3,2))
barplot(matematicas[[1]],names.arg=1:6,main="Matematicas",sub="(grupo caso)")
barplot(matematicas[[2]],names.arg=1:6,main="Matematicas",sub="(grupo control)")
barplot(ingles[[1]],names.arg=1:6,main="Ingles",sub="(grupo caso)")
barplot(ingles[[2]],names.arg=1:6,main="Ingles",sub="(grupo control)")
barplot(noruego[[1]],names.arg=1:6,main="Noruego",sub="(grupo caso)")
barplot(noruego[[2]],names.arg=1:6,main="Noruego",sub="(grupo control)")
graphics.off()
matematicas <- data.frame (caso = c(0.01,0.16,0.30,0.31,0.19,0.03),
control = c(0.01,0.05,0.26,0.43,0.22,0.03) )
ingles <- data.frame(caso = c(0.01,0.08,0.25,0.40,0.24,0.02),
control = c(0.00,0.05,0.21,0.43,0.27,0.04) )
noruego <- data.frame(caso = c(0.00,0.05,0.25,0.46,0.24,0.00),
control = c(0.00,0.03,0.24,0.45,0.26,0.02) )
graficar_barras_divergentes <- function(mdata,nombre=deparse(substitute(mdata))) {
#esta función supone que mdata es un marco de datos
#en donde cada columna se asocia a los porcentajes de los niveles
#de una escala ordinal en orden ascendente (ie. el primer elemento del
#vector se corresponde a la frecuencia del menor nivel en la escala).
mdata_ac <- rbind(mdata,rep(0,ncol(mdata)))
filas_par <- (nrow(mdata) %% 2 == 0)
for (i in 1:ncol(mdata)) {
x <- cumsum(mdata[[i]])
if (filas_par)
mid <- x[nrow(mdata) %/% 2]
else
mid <- x[nrow(mdata) %/% 2] + mdata[[i]][(nrow(mdata) %/% 2) + 1]/2
mdata_ac[[i]] <- c(-mid,x -mid)
}
#crea un nuevo cuadro del tamaño adecuado
frame()
plot.window(xlim=c(min(mdata_ac)-0.2,max(mdata_ac)),ylim=c(0,0.5*ncol(mdata_ac)))
#dibuja una línea vertical punteada de "centralidad"
lines(c(0,0),c(0,0.5*ncol(mdata_ac)),lty="dotted")
for (i in 1:ncol(mdata_ac) ) {
#calcula la posición de las etiquetas para las frecuecias/categorias
lbx <- (tail(mdata_ac[[i]],-1)+head(mdata_ac[[i]],-1))/2
#dibuja los rectángulos que componen las frecuencias de cada clase
for (j in 1:(nrow(mdata_ac)-1) )
rect(mdata_ac[j,i], 0.21 + (i-1)*0.5 ,mdata_ac[j+1,i], 0.29 + (i-1)*0.5 ,
col=rgb(95/256,158/256,160/256,alpha=mdata[j,i]) , lwd=0.25 )
#escribe las frecuencias
text(x=lbx,y=0.18+(i-1)*0.5,cex=0.4,labels=round(mdata[[i]]*100,digits=2) )
#escribe las etiquetas de categorías
text(x=lbx, y=0.32+(i-1)*0.5,cex=0.4,labels=rownames(mdata) )
#indica los cuartiles
#indica cuartiles
points(seq(from=0.25,to=0.75,by=0.25)+mdata_ac[1,i],rep(0.25+(i-1)*0.5,3),col="tomato",pch=10)
}
#escribe las etiquetas de cada serie de datos
text(x=min(mdata_ac)-0.1,y=seq(from=0.25,to=0.25+0.5*ncol(mdata),by=0.5),cex=0.8,labels=colnames(mdata) )
#El titulo
title(main=paste("Gráfica de barras divergentes para\n",nombre) )
}
ppi <- 300
png("gbd%2d.png",width=ppi*4,height=ppi*4,res=ppi)
graficar_barras_divergentes(matematicas)
graficar_barras_divergentes(ingles)
graficar_barras_divergentes(noruego)
graphics.off()
png("graficos_de_barras.png",width=ppi*4,height=ppi*6,res=ppi)
par(mfrow=c(3,2))
barplot(matematicas[[1]],names.arg=1:6,main="Matematicas",sub="(grupo caso)")
barplot(matematicas[[2]],names.arg=1:6,main="Matematicas",sub="(grupo control)")
barplot(ingles[[1]],names.arg=1:6,main="Ingles",sub="(grupo caso)")
barplot(ingles[[2]],names.arg=1:6,main="Ingles",sub="(grupo control)")
barplot(noruego[[1]],names.arg=1:6,main="Noruego",sub="(grupo caso)")
barplot(noruego[[2]],names.arg=1:6,main="Noruego",sub="(grupo control)")
graphics.off()
Bibliografía
- HASSAN, J. (2007). Parents’ socioeconomic status and children’s academic performance. Norwegian Social Research. NOVA Notat 7/2009.
- HEIBERGER, R. y ROBBINS, N. (2011). Plotting Likert and Other Rating Scales Section on Survey Research Methods – JSM 2011.
Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.
martes, 25 de diciembre de 2012
Consideraciones sobre la visualización de datos- parte 1
Este semestre, he visto algunos trabajos de Estadística General (745) en los cuales se incluyen las famosas gráficas de torta tridimensionales. Aunque en el sitio anterior de unamatematicaseltigre había escrito sobre esto, vuelvo a publicar el post original en esta página agregándole otras aclaratorias. Esta será la primera de una serie de entradas sobre las técnicas de visualización alternativas o más adecuadas para la data cualitativa, que es la materia prima de la denominada "investigación cualitativa" de las humanidades y las ciencias sociales. Estudiantes de educación, estudiantes de administración y contaduría, este tema es de interés para ustedes. Trataré de mantener el contenido matemático al mínimo necesario para hacer su lectura menos árida. Pero antes, permítanme expresarles mi opinión sobre las gráficas de torta tridimensionales. Iré directamente al grano: las gráficas de torta tridimensionales son malas. No sirven.
¿Porqué no sirven las gráficas de torta tridimensionales? ¿No indican también el 100% de los datos?
El propósito de las gráficas de torta es comunicar visualmente las proporciones que se corresponden a los tamaños de varios subgrupos dentro de una población. Para poder elaborar una gráfica de torta, se supone que:
- Tenemos una variable con una cantidad determinada de valores o atributos que esta puede asumir en la población bajo estudio.
- Cada individuo de la población se asocia a exactamente uno entre los atributos de la variable. Un individuo no puede asociarse a dos o más de estos atributos. Por ejemplo, si la variable es el género, cada uno de los individuos de la población bajo estudio, o es de sexo masculino o de sexo femenino, pero no hay individuos de ambos sexos o ninguno.
- Podemos clasificar a la totalidad de la población en grupos de individuos con el mismo atributo de la variable y calcular el porcentaje de la cantidad total de individuos correspondientes a cada uno de esos grupos. Aunque parezca obvio, hay que enfatizar que las gráficas de torta siempre se refieren a la distribución del 100% de la población en varios subgrupos según los atributos de una variable.
Con respecto a la última observación, quiero traer a colación una gráfica de torta que apareció en un noticiero norteamericano. El propósito de esta gráfica era mostrar cuantos encuestados apoyaban a determinado candidato para las elecciones primarias del partido Republicano en Estados Unidos:

La característica más deplorable de esta gráfica es que los porcentajes suman a 193%. Obviamente, la encuesta fue hecha de forma que los encuestados podían responder que apoyaban a más de un candidato (algunos quizás a los tres candidatos, inclusive). Sin embargo, el uso de una gráfica de torta para visualizar los resultados de tal encuesta es sencillamente equivocado. Por definición, una gráfica de torta muestra los porcentajes de las categorías en base al 100% de la data porque se supone que las categorías son mutuamente excluyentes y cada uno de los individuos de la población se asocia a una sola categoría. Esto excluiría la posibilidad de que algún encuestado responda que apoya a Pallin y a Romney, por ejemplo. Consecuentemente, el uso de una gráfica de torta para esta encuesta queda descartado y deja muchas incógnitas sin responder: ¿cuantos encuestados apoyan únicamente a uno de los tres candidatos del partido? ¿cuantos encuestados no apoyan a ninguno de los tres candidatos?
No se me ocurre de buenas a primeras una buena alternativa a la gráfica de torta para la visualización de los resultados de esta encuesta. Todo depende de la "idea" que realmente se quiere comunicar. Quizás los comunicadores sociales tenían simpatías hacia Pallin y consecuentemente mostraron una gráfica según la cual la "mayoría" apoyaba a esta candidata, aunque hay otros elementos en la gráfica que refutan esa idea (volveré sobre ese tema más adelante en esta entrada). Es posible que si mostrasen los resultados correspondientes a cuantos de entre los encuestados que apoyaban a un único candidato, apoyaban a Pallin, Romney o Huckabee, la gráfica hubiese sido muy distinta, pero por lo menos hubiese sido una gráfica de torta legítima (porque las categorías en este caso sí son mutuamente excluyentes).
Bien, aún no he abordado el tema inicial de esta entrada: ¿porqué no sirven las gráficas de torta 3d? La gráfica de torta permite visualizar los porcentajes de cada categoría mediante la comparación visual del tamaño respectivo de los pedazos de la torta. Es decir, la lectura de una gráfica de tortas consiste en comparar el área o la magnitud de distintas superficies y en esto el ojo humano no es particularmente eficaz. Considere por ejemplo esta gráfica:

Viendo la gráfica de arriba, intente responder las siguientes interrogantes: ¿Cual de las dos categorías, azul (2) o roja (1), tiene mayor porcentaje? ¿Podría usted ordenar la categoría negra (5), verde (3) y amarilla (4) de mayor a menor porcentaje? La respuesta a estas preguntas se hace más evidente al observar el diagrama de barras equivalente:

Insisto- el diagrama de barras de arriba es equivalente a la gráfica de torta anterior; ambos se elaboraron con la misma data. Sin embargo, el diagrama de barras visualiza mejor las diferencias entre las proporciones de cada categoría. ¿Porqué?
Es más fácil comparar longitudes que superficies. Mientras mayor dimensionalidad, más difícil se hace establecer las comparaciones. Por esta razón, muchos especialistas desaconsejan el uso de gráficas de torta. Algunos inclusive las detestan:
Las tablas son preferibles a las gráficas para conjuntos pequeños de data. Una tabla es casi siempre mejor que una estúpida gráfica de torta; lo único peor que una gráfica de torta es varias de ellas, pues entonces se requiere que el lector compare magnitudes ubicadas desordenadamente tanto dentro de las tortas como entre las tortas. Dada su baja densidad de data y la ineficacia en ordenar magnitudes a lo largo de una dimensión visual, las gráficas de torta nunca deberían ser empleadas."
The Visualization of Quantitative Information, p. 178
Edward Tufte
No queriendo asumir una posición tan radical en torno a las gráficas de torta y admitiendo que aún en ciertos casos pueden ser de alguna utilidad, mi idea es advertir sobre algunos problemas en el uso de este tipo de gráficas. Como regla general, la comparación de magnitudes se dificulta a medida que las visualizamos en más dimensiones. Con las gráficas de torta tridimensionales yo trazo la línea- nunca deberían de utilizarse. Considere por ejemplo, este par de gráficas tridimensionales referidas a las elecciones parlamentarias del 2010 en Venezuela, en la cual se visualizan los porcentajes de votos atribuidos al oficialismo y a la oposición.
 |
 |
Ambas gráficas visualizan los mismos resultados: el 52% de los votos fueron para la oposición y el 48% de los votos para el oficialismo. Sin embargo, como las graficas se presentan en perspectiva (tridimensional), la percepción que inducen sobre el lector es muy distinta- en la gráfica de la izquierda, el oficialismo parece haberse hecho con la mayoría de los votos mientras que en la gráfica de la derecha, la oposición luce con una mayoría abrumadora. Al examinar ambas gráficas a la luz de los porcentajes en base a los cuales fueron elaboradas (52 y 48 porciento), se hace evidente que ninguna presenta la información de manera objetiva, pese a que (insisto sobre ello) fueron elaboradas en base a los mismos porcentajes.
Cuando representamos objetos tridimensionales sobre una superficie bidimensional, los objetos que están ubicados hacia adelante lucen mayores que los que están ubicados atrás, por razones de perspectiva. Las gráficas de torta tridimensionales siempre serán engañosas porque las categorías presentadas al frente lucirán un poco más grandes que las categoráas al fondo de la gráfica. Aunque se coloquen los porcentajes sobre cada sector, podemos engañar al lector según la o las categorías que presentamos en primer plano en una gráfica de torta 3D. Con esto volvemos a la gráfica de torta tridimensional de Foxnews presentada al principio de esta entrada. Habíamos especulado sobre la posible intención del noticiero de promover a la candidata Pallin como mayoritaria, según la definición de las categorías utilizada para construir la gráfica (que no era apropiada puesto que no sumaban a un 100%). Sin embargo, en vista de que los otros dos candidatos se presentan en colores similares (azul y verde) hacia el primer plano de una gráfica 3d ligeramente inclinada, quizás se quería lo contrario: promover a los otros dos candidatos distintos a Pallin. Personalmente, no creo que quien elaboró la gráfica tenía con alguna intención o agenda oculta- simplemente ignoró los principios básicos de la estadística descriptiva y el sentido común.
Referencias bibliográficas
- Kosara, R. (12/01/2012). Understanding Pie Charts. Publicado en: http://eagereyes.org/techniques/pie-charts
- Tufte, E. (2001). The Visualization of Quantitative Information. Second Edition. Graphic Press.
- Yau, N. (26/11/2009). Fox News Makes the Best Pie Chart. Ever. Publicado en: http://flowingdata.com/2009/11/26/fox-news-makes-the-best-pie-chart-ever/
Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.
Suscribirse a:
Comentarios (Atom)


