miércoles, 4 de abril de 2018
Charla introductoria sobre criptomonedas
viernes, 20 de octubre de 2017
Talleres lapso 2017-2
Matematicas I (175-176-177)
Estadística General (745)
| Día | Hora - Lugar | Contenido |
| 28/10/2017 | 9:30am sede UNA El Tigre | Objetivos 1-4 |
| 02/12/2017 | 9:30am sede UNA El Tigre | Objetivos 5-8 |
| 10/02/2018 | 9:30am sede UNA El Tigre | Objetivos 1-8 |
Estadística Aplicada (746)
| Día | Hora - Lugar | Contenido |
| 04/11/2017 | 9:30am sede UNA El Tigre | Objetivos 1-4 |
| 09/12/2017 | 9:30am sede UNA El Tigre | Objetivos 5-8 |
| 17/02/2018 | 9:30am sede UNA El Tigre | Objetivos 1-8 |
lunes, 1 de mayo de 2017
Aventura de Regresión Lineal y el método de eliminación hacia atrás paso a paso
En esta entrada, haremos el ejercicio de regresión lineal planteado en el semestre 2012-1, cuyo trabajo práctico es igual al de este semestre (2017-1). Se hace uso del R y mi librería estUNA para construir modelos de regresión lineal mediante el método de eliminación hacia atrás. En este proceso, enfatizamos la importancia de realizar un análisis de residuos, entre otras cosas para sugerirnos posibles transformaciones de las variables con las que podamos mejorar los modelos de regresión.
miércoles, 19 de abril de 2017
Algunos comentarios sobre el valor absoluto (Objetivo 3 de Matemática I)
jueves, 6 de abril de 2017
estUNA
¿Qué es estUNA?
Eventualmente será publicada en el repositorio CRAN como un paquete. Actualmente, el archivo imagen (que permite trabajar con la librería) está disponible para su descarga en https://raw.githubusercontent.com/unamatematicaseltigre/estUNA/master/estUNA.
Introducción al R
 es un entorno de programación
es un entorno de programación
En esta página se hará una brevísima introducción al lenguaje R como entorno de programación. Sin pretender que esto sea una guía completa, se exponen los conceptos necesarios para poder utilizar este lenguaje como complemento instruccional a los cursos de estadística y probabilidades de la Universidad Nacional Abierta.
Un entorno de programación es una aplicación que permite crear, ejecutar y depurar programas. Los programas son esencialmente secuencias de instrucciones que le indican al computador de manera muy precisa lo que este debe hacer. Estas instrucciones se especifican en algo llamado lenguaje de programación y cada lenguaje de programación tiene su "gramática" particular y sus reglas de sintaxis. R es un lenguaje de programación interpretado, lo cual quiere decir que el programador ingresa instrucciones a través de una consola y el interprete de R va procesando cada instrucción a medida que esta se ingresa y va dando la salida respectiva a cada instrucción de forma secuencial.
En vez de escribir las instrucciones una por una en la consola, podemos indicar la secuencia de instrucciones que queremos ejecutar a través de un archivo de texto (cómo los que creamos cuando usamos el bloc de notas). Esto es lo que se conoce como un script. Un script es una especie de programa que necesita siempre de un interprete para poderse ejecutar. En esta guía, aprenderemos a crear nuestros propios scripts.
viernes, 17 de febrero de 2017
Talleres para el Lapso 2017-1
Matematicas I (175-176-177)
Estadística General (745)
| Día | Hora - Lugar | Contenido |
| 04/03/2017 | 9:30am sede UNA El Tigre | Objetivos 1-4 |
| 01/04/2017 | 9:30am sede UNA El Tigre | Objetivos 5-8 |
| 27/05/2017 | 9:30am sede UNA El Tigre | Objetivos 1-8 |
Estadística Aplicada (746)
| Día | Hora - Lugar | Contenido |
| 11/03/2017 | 9:30am sede UNA El Tigre | Objetivos 1-4 |
| 29/04/2017 | 9:30am sede UNA El Tigre | Objetivos 5-8 |
| 03/06/2017 | 9:30am sede UNA El Tigre | Objetivos 1-8 |
viernes, 6 de enero de 2017
Retrospectiva de unamatematicaseltigre 2016
viernes, 23 de diciembre de 2016
Feliz Navidad 2016 (en R)
plot3D de R:
domingo, 11 de diciembre de 2016
La Era de la Información: ¿Ilustración o Ignorancia?
domingo, 20 de noviembre de 2016
Telemercadeo por correo electrónico usando R
viernes, 7 de octubre de 2016
La Matemática es Fácil - canal de YouTube del Profesor José Gascón
martes, 27 de septiembre de 2016
Introducción al LaTeX, o cómo escribir formulas matemáticas cuando quieran plantearme una duda por correo
jueves, 8 de septiembre de 2016
Andragogía de las matematicas y el método de Anat Baniel

jueves, 18 de agosto de 2016
Resolución de problemas matemáticos (o ¿qué busco yo como asesor en una respuesta?)
domingo, 31 de julio de 2016
¿En qué consiste la inferencia estadística? Protocolo de inferencia estadística - parte 1
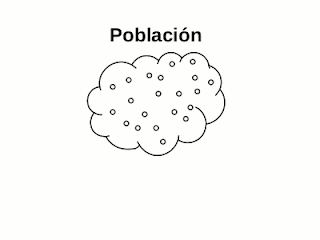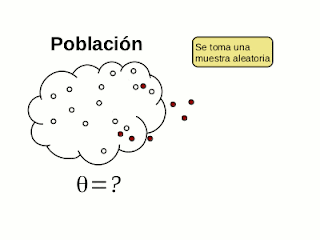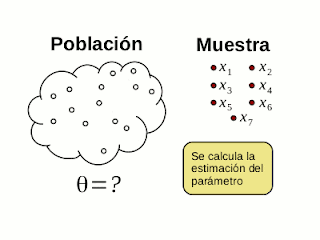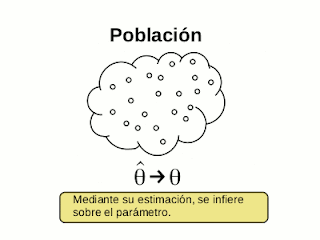
lunes, 25 de julio de 2016
Trabajo práctico de la 745, lapso 2016-1
jueves, 21 de julio de 2016
Métodos de Redondeo (Objetivo 1 de Matemáticas I)
martes, 19 de julio de 2016
Trabajos de Estadística (738/748, 745 y 746) Lapso 2016-1
| 738/748 |
| 745 |
| 746 |
Para este semestre, la data se encuentra en el siguiente data frame de estUNA: d20161
Si te gustó o te pareció útil este contenido, compártelo en las redes sociales y dale tu voto positivo en el botón "me gusta" de G+, para que otros puedan encontrar el contenido también.
miércoles, 15 de junio de 2016
Talleres para el semestre 2016-1
Matemática I (175-176-177)
| Taller 1 | Inducción | 25/06/2016 | 8am-12pm |
| Taller 2 | Unidades 1 y 2 | 02/07/2016 | 8am-12am |
| Taller 3 | Unidades 3 y 4 | 09/07/2016 | 2-5pm |
| Taller 4 | Unidades 5 y 6 | 16/07/2016 | 8am-12pm |
| Taller 5 | Unidad 7 | 02/09/2016 | 8am (sede UNA) |
| Taller 6 | 03/09/2016 | 8am (sede UNA) |
Los talleres de Matemática I serán dictados en el Trujillo. Estén atentos a la publicación de fechas de los siguientes talleres.
Estadística General (745)
| Taller 1 | Objetivos 1-4 | 16/07/2016 | 9am-12pm |
| Taller 2 | Objetivos 5-8 | 17/09/2016 | 9am-12pm |
| Taller 3 | Objetivos 1-8 | 22/10/2016 | 9am-12pm |
| Taller 4 | Objetivos 1-8 | 05/11/2016 | 9am-12am |
Estadística Aplicada (746)
| Taller 1 | Objetivos 1-4 | 23/07/2016 | 9am-12pm |
| Taller 2 | Objetivos 5-8 | 24/09/2016 | 9am-12pm |
| Taller 3 | Objetivos 1-8 | 29/10/2016 | 9am-12pm |
| Taller 4 | Objetivos 1-8 | 12/11/2016 | 9am-12pm |
